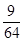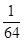题目内容
某中学校本课程共开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生:
(1)求这3名学生选修课所有选法的总数;
(2)求恰有2门选修课没有被这3名学生选择的概率;
(3)求A选修课被这3名学生选择的人数的数学期望.
【答案】
(1)64(2) (3)
(3)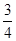
【解析】
试题分析:解析:(Ⅰ)每个学生有四个不同选择,根据乘法法则,选法总数N=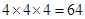 3分
3分
(Ⅱ) 恰有2门选修课这3名学生都没选择的概率为
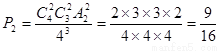 7分
7分
(Ⅲ) 设A选修课被这3名学生选择的人数为 ,则
,则 =0,1,2,3
=0,1,2,3
P( =0)=
=0)= P(
P( =1)=
=1)=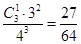
P( =2)=
=2)=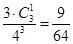 P(
P( =3)=
=3)=
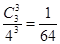 9分
9分
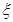 的分布列是
的分布列是
|
|
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
10分
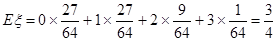 12分
12分
考点:古典概型的概率
点评:主要是考查了分布列和数学期望值的求解,主要是解决运用古典概型的概率公式来求解概率值,属于基础题。

练习册系列答案
相关题目