题目内容
一个等比数列的前n项之和是2n-b,那么它的前n项的各项平方之和为( )
分析:设该等比数列为{an},前n项和为Sn=2n-b,求出数列的前3项,利用等比数列的性质可得关于b的方程,解出b可求得an,易判断数列各项的平方仍构成等比数列,从而可求得答案.
解答:解:设该等比数列为{an},前n项和为Sn=2n-b,
则a1=2-b,a2=S2-S1=2,a3=S3-S2=4,
∴22=(2-b)×4,解得b=1,
∴该数列的首项为1,公比为2,
∴an=2n-1,则an2=22n-2,
又
=
=4(常数),
∴{an2}是首项为1,公比为4的等比数列,
∴原等比数列的前n项的各项平方之和为:12+22+42+…+22n-2=
=
(4n-1),
故选D.
则a1=2-b,a2=S2-S1=2,a3=S3-S2=4,
∴22=(2-b)×4,解得b=1,
∴该数列的首项为1,公比为2,
∴an=2n-1,则an2=22n-2,
又
| an+12 |
| an2 |
| 22n |
| 22n-2 |
∴{an2}是首项为1,公比为4的等比数列,
∴原等比数列的前n项的各项平方之和为:12+22+42+…+22n-2=
| 1-4n |
| 1-4 |
| 1 |
| 3 |
故选D.
点评:本题考查等比数列的前n项和、等比数列的通项公式,考查学生的运算求解能力,熟记相关通项公式、求和公式是解决问题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
一个等比数列的前n项和Sn=a-(
)n,则该数列的各项和近似为( )
| 1 |
| 2 |
A、
| ||
| B、1 | ||
C、-
| ||
| D、2 |
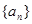 的前n项和为48,前2n项和为60,则前3n项和为( )
的前n项和为48,前2n项和为60,则前3n项和为( )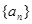 的前n项和为48,前2n项和为60,则前3n项和为( )
的前n项和为48,前2n项和为60,则前3n项和为( )