题目内容
(本题12分)设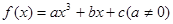 为奇函数,其图象在点
为奇函数,其图象在点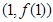 处的切线与直线
处的切线与直线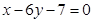 垂直,导函数
垂直,导函数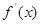 的最小值为
的最小值为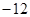 .
.
(1)求函数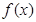 的解析式;
的解析式;
(2)求函数f(x)在[-1,3]上的最大值和最小值.
【答案】
解:(1)∵f(x)为奇函数,∴f(-x)=-f(x),即-ax3-bx+c=-ax3-bx-c,∴c=0.
又f′(x)=3ax2+b的最小值为-12,∴b=-12.
由题设知f′(1)=3a+b=-6,∴a=2,
故f(x)=2x3-12x. (6分)
(2)f′(x)=6x2-12=6(x+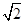 )(x-
)(x-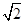 ),当x变化时,f′(x)、f(x)的变化情况表如下:
),当x变化时,f′(x)、f(x)的变化情况表如下:
|
x |
(-∞,- |
- |
(- |
|
( |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
|
极大值 |
|
极小值 |
|
∴函数f(x)的单调递增区间为(-∞,-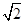 )和(
)和(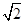 ,+∞),
,+∞),
∵f(-1)=10,f(3)=18,f(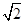 )=-8
)=-8 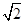 ,f(-
,f(-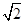 )=8
)=8 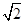 ,
,
当x=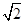 时,f(x)min=-8
时,f(x)min=-8 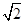 ;当x=3时,f(x)max=18. (12分)
;当x=3时,f(x)max=18. (12分)
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ?
? ?
? ?
?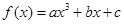
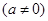 为奇函数,其图象在点
为奇函数,其图象在点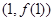 处的切线与直线
处的切线与直线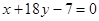 垂直,导函数
垂直,导函数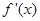 的最小值为
的最小值为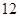 .
.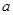 ,
,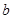 ,
,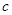 的值;
的值;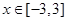 时,
时,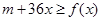 恒成立,求
恒成立,求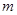 的范围;
的范围;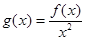 ,当
,当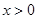 时,求
时,求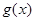 的最小值.
的最小值.