题目内容

已知椭圆的中心在原点，它在x轴上的一个焦点与短轴两端点连线互相垂直，且此焦点和x轴上的较近端点的距离为4（
2
-1），求椭圆方程．
∵椭圆的中心在原点，焦点在x轴上，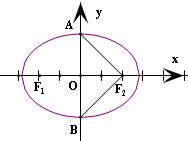
∴设椭圆的方程为
x2
a2
+
y2
b2
=1（a＞b＞0），
设短轴的两个端点分别为A、B，左右焦点分别为F1、F2，连结AF2、BF2．
∵一个焦点与短轴两端点连线互相垂直，
∴AF2⊥BF2，
根据椭圆的对称性得到△ABF2是等腰直角三角形，可得|OA|=|0F2|．
∴b=c，即
a2-c2
=c…①，
又∵焦点和x轴上的较近端点的距离为4（
2
-1），
∴a-c=4（
2
-1）…②，
联解①②可得a=4
2
，c=4，可得a2=32，b2=c2=16
所求椭圆的方程为
x2
32
+
y2
16
=1．
练习册系列答案
相关题目
曲线
x2
25
+
y2
16
=1与曲线
x2
25+k
+
y2
16+k
=1（k＞-16）的（　　）
A．长轴长相等B．短轴长相等C．离心率相等D．焦距相等
过点（-3，2）且与
x2
9
+
y2
4
=1有相同焦点的椭圆的方程是（　　）
A．
x2
15
+
y2
10
=1		B．
x2
225
+
y2
100
=1
C．
x2
10
+
y2
15
=1		D．
x2
100
+
y2
225
=1
已知θ为斜三角形的一个内角，曲线F：x2sin2θcos2θ+y2sin2θ=cos2θ是（　　）
A．焦点在x轴上，离心率为sinθ的双曲线
B．焦点在x轴上，离心率为sinθ的椭圆
C．焦点在y轴上，离心率为|cosθ|的双曲线
D．焦点在y轴上，离心率为|cosθ|的椭圆
已知椭圆C1，抛物线C2的焦点均在y轴上，C1的中心和C2的顶点均为坐标原点O，从每条曲线上取两个点，将其坐标记录于下表中：
x0-1
2
4
y-2
2
1
16
-21
（Ⅰ）求分别适合C1，C2的方程的点的坐标；
（Ⅱ）求C1，C2的标准方程．
设m是正实数．若椭圆
x2
m2+16
+
y2
9
=1的焦距为8，则m=______．
设F1，F2分别是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点，若在直线x=
a2
c
上存在点P，使线段PF1的中垂线过点F2，则椭圆的离心率的取值范围是______．
求以椭圆
x2
16
+
y2
9
=1的短轴的两个端点为焦点，且过点A（4，-5）的双曲线的标准方程．
简化的北京奥运会主体育场“鸟巢”的钢结构俯视图如图所示，内外两圈的钢骨架是离心率相同的椭圆，外层椭圆顶点向内层椭圆引切线AC，BD，设内层椭圆方程为
x2
a2
+
y2
b2
=1(a＞b＞0)，则外层椭圆方程可设为
x2
(ma)2
+
y2
(mb)2
=1(a＞b＞0，m＞1)．若AC与BD的斜率之积为-
9
16
，则椭圆的离心率为（　　）
A．
7
4
B．
2
2
C．
6
4
D．
3
4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网