题目内容
8.已知函数f(x6)=log2x.(1)求f(x)的解析式;
(2)求f($\frac{1}{8}$).
分析 (1)令x6=t,则x=$\root{6}{t}$,换元可得f(t)=$\frac{1}{6}$log2t,可得f(x)=$\frac{1}{6}$log2x;
(2)把x=$\frac{1}{8}$代入f(x)=$\frac{1}{6}$log2x,由对数的性质化简可得.
解答 解:(1)令x6=t,则x=$\root{6}{t}$,
换元可得f(t)=log2$\root{6}{t}$=$\frac{1}{6}$log2t,
∴f(x)=$\frac{1}{6}$log2x;
(2)由(1)可得f(x)=$\frac{1}{6}$log2x,
∴f($\frac{1}{8}$)=$\frac{1}{6}$log2$\frac{1}{8}$=$\frac{1}{6}×(-3)$=-$\frac{1}{2}$
点评 本题考查函数解析式求解的换元法,涉及对数的运算,属基础题.

练习册系列答案
相关题目
13.已知(x2+$\frac{1}{x}$)6的展开式中的常数项为a,则直线y=ax与曲线y=x3围成的封闭图形的面积为( )
| A. | 450 | B. | 225 | C. | $\frac{225}{2}$ | D. | $\frac{225}{4}$ |
20.函数y=$\frac{1-a}{x}$(a≠1)在(-∞,0),(0,+∞)上是增函数,则实数a的取值范围是( )
| A. | (-∞,1)∪(1,+∞) | B. | (-∞,0) | C. | (-∞,1) | D. | (1,+∞) |
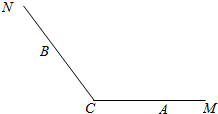 已知点A,B分别在射线CM,CN(不含端点C)上运动,∠MCN=$\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c
已知点A,B分别在射线CM,CN(不含端点C)上运动,∠MCN=$\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c