题目内容
设定义在 上的函数
上的函数 满足
满足 ,若
,若 ,则
,则
A. | B. | C. | D. |
C
解析试题分析:利用题中条件:“f(x)•f(x+2)=13”得出函数f(x)是周期函数,从而利用f(1)的值求出f(99)即可.
∵f(x)•f(x+2)=13∴f(x+2)•f(x+4)=13,
∴f(x+4)=f(x),∴f(x)是一个周期为4的周期函数,
∴f(99)=f(4×25-1)=f(-1)=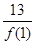 =
= .
.
故答案为: ,故选C.
,故选C.
考点:本题主要考查抽象函数的周期性的运用,以及赋值思想的运用。主要考查了抽象函数及其应用,考查分析问题和解决问题的能力,属于中档题
点评:解决该试题的关键是函数的周期性是高考函数题的重点考查内容,几个重要的周期公式要熟悉,如:(1)f(x+a)=f(x-a),则T=2a;(2)f(x+a)=- ,则T=2a等.
,则T=2a等.

练习册系列答案
相关题目
下列函数为偶函数且在 上为增函数的是( )
上为增函数的是( )
A. | B. | C. | D. |
已知函数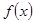 是偶函数,其图像与
是偶函数,其图像与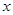 轴有四个不同的交点,则函数
轴有四个不同的交点,则函数 的所
的所
有零点之和为( )
| A.0 | B.8 | C.4 | D.无法确定 |
下列各组函数中,表示同一个函数的是
A. 与 与 | B. 与 与 |
C. 与 与 | D. 与 与 |
设 为实数,则
为实数,则 与
与 表示同一个函数的是 ( )
表示同一个函数的是 ( )
A. | B. |
C. | D. |
若 ,则
,则 的定义域为
的定义域为
A. | B. | C. | D. |
已知数列 满足:
满足: ,则
,则 =( )
=( )
A. | B. | C. | D. |
在区间 上为增函数的是( )
上为增函数的是( )
A. | B. |
C. | D. |
 ,
,  ,则
,则 的图象只可能是( )
的图象只可能是( )