题目内容
长度为a(a>0)的线段AB的两个端点A、B分别在x轴和y轴上滑动,点P在线段AB上,且 (λ为常数且λ>0).
(λ为常数且λ>0).(Ⅰ)求点P的轨迹方程C;
(Ⅱ)当a=λ+1时,过点M(1,0)作两条互相垂直的直线l1和l2,l1和l2分别与曲线C相交于点N和Q(都异于点M),试问:△MNQ能不能是等腰三角形?若能,这样的三角形有几个;若不能,请说明理由.
【答案】分析:(I)欲求点P的轨迹方程,设点P(x,y),只须求出其坐标x,y的关系式即可,由题意知点P满足于 得到一个关系式,再结合线段AB的长度为a(a>0),化简即得点P的轨迹方程;
得到一个关系式,再结合线段AB的长度为a(a>0),化简即得点P的轨迹方程;
(Ⅱ)当a=1+λ时,曲线C的方程为 .依题意,直线l1和l2均不可能与坐标轴平行,故不妨设直线l1:x=my+1(m>0),直线
.依题意,直线l1和l2均不可能与坐标轴平行,故不妨设直线l1:x=my+1(m>0),直线 ,与曲线方程联立,可求|MN|,|MQ|,若△MNQ是等腰三角形,则|MN|=|MQ|,由此可得(m-1)[m2+(1-λ2)m+1]=0,即m=1或m2+(1-λ2)m+1=0.讨论方程m2+(1-λ2)m+1=0的根的情形,即可得到满足条件的三角形的个数.
,与曲线方程联立,可求|MN|,|MQ|,若△MNQ是等腰三角形,则|MN|=|MQ|,由此可得(m-1)[m2+(1-λ2)m+1]=0,即m=1或m2+(1-λ2)m+1=0.讨论方程m2+(1-λ2)m+1=0的根的情形,即可得到满足条件的三角形的个数.
解答:解:(Ⅰ)设P(x,y)、A(x,0)、B(0,y),则
 ,
,
由此及 得
得 ,
,
即 ;
;
(Ⅱ)当a=1+λ时,曲线C的方程为 .
.
依题意,直线l1和l2均不可能与坐标轴平行,故不妨设直线l1:x=my+1(m>0),直线 ,从而有
,从而有 .
.
同理,有 .
.
若△MNQ是等腰三角形,则|MN|=|MQ|,由此可得(m-1)[m2+(1-λ2)m+1]=0,即m=1或m2+(1-λ2)m+1=0.
下面讨论方程m2+(1-λ2)m+1=0的根的情形(△=(λ2+1)(λ2-3)):
①若 ,则△<0,方程没有实根;
,则△<0,方程没有实根;
②若 ,则△=0,方程有两个相等的实根m=1;
,则△=0,方程有两个相等的实根m=1;
③若 ,则△>0,方程有两个相异的正实根,且均不等于1(因为12+(1-λ2)•1+1=3-λ2≠0).
,则△>0,方程有两个相异的正实根,且均不等于1(因为12+(1-λ2)•1+1=3-λ2≠0).
综上所述,△MNQ能是等腰三角形:当 时,这样的三角形有且仅有一个;当
时,这样的三角形有且仅有一个;当 时,这样的三角形有且仅有三个.
时,这样的三角形有且仅有三个.
点评:本题考查的重点是轨迹方程,考查分类讨论的数学思想,解题的关键是将直线方程与曲线方程联立,利用方程根的讨论,确定满足条件的三角形的个数.
 得到一个关系式,再结合线段AB的长度为a(a>0),化简即得点P的轨迹方程;
得到一个关系式,再结合线段AB的长度为a(a>0),化简即得点P的轨迹方程;(Ⅱ)当a=1+λ时,曲线C的方程为
 .依题意,直线l1和l2均不可能与坐标轴平行,故不妨设直线l1:x=my+1(m>0),直线
.依题意,直线l1和l2均不可能与坐标轴平行,故不妨设直线l1:x=my+1(m>0),直线 ,与曲线方程联立,可求|MN|,|MQ|,若△MNQ是等腰三角形,则|MN|=|MQ|,由此可得(m-1)[m2+(1-λ2)m+1]=0,即m=1或m2+(1-λ2)m+1=0.讨论方程m2+(1-λ2)m+1=0的根的情形,即可得到满足条件的三角形的个数.
,与曲线方程联立,可求|MN|,|MQ|,若△MNQ是等腰三角形,则|MN|=|MQ|,由此可得(m-1)[m2+(1-λ2)m+1]=0,即m=1或m2+(1-λ2)m+1=0.讨论方程m2+(1-λ2)m+1=0的根的情形,即可得到满足条件的三角形的个数.解答:解:(Ⅰ)设P(x,y)、A(x,0)、B(0,y),则
 ,
,由此及
 得
得 ,
,即
 ;
;(Ⅱ)当a=1+λ时,曲线C的方程为
 .
.依题意,直线l1和l2均不可能与坐标轴平行,故不妨设直线l1:x=my+1(m>0),直线
 ,从而有
,从而有 .
.同理,有
 .
.若△MNQ是等腰三角形,则|MN|=|MQ|,由此可得(m-1)[m2+(1-λ2)m+1]=0,即m=1或m2+(1-λ2)m+1=0.
下面讨论方程m2+(1-λ2)m+1=0的根的情形(△=(λ2+1)(λ2-3)):
①若
 ,则△<0,方程没有实根;
,则△<0,方程没有实根;②若
 ,则△=0,方程有两个相等的实根m=1;
,则△=0,方程有两个相等的实根m=1;③若
 ,则△>0,方程有两个相异的正实根,且均不等于1(因为12+(1-λ2)•1+1=3-λ2≠0).
,则△>0,方程有两个相异的正实根,且均不等于1(因为12+(1-λ2)•1+1=3-λ2≠0).综上所述,△MNQ能是等腰三角形:当
 时,这样的三角形有且仅有一个;当
时,这样的三角形有且仅有一个;当 时,这样的三角形有且仅有三个.
时,这样的三角形有且仅有三个.点评:本题考查的重点是轨迹方程,考查分类讨论的数学思想,解题的关键是将直线方程与曲线方程联立,利用方程根的讨论,确定满足条件的三角形的个数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
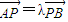 (λ为常数且λ>0).
(λ为常数且λ>0).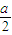 ,且直线l1与轨迹C有公共点,求直线l1的斜率k的取值范围.
,且直线l1与轨迹C有公共点,求直线l1的斜率k的取值范围. (λ为常数且λ>0).
(λ为常数且λ>0). ,且直线l1与轨迹C有公共点,求直线l1的斜率k的取值范围.
,且直线l1与轨迹C有公共点,求直线l1的斜率k的取值范围.