题目内容
长度为a(a>0)的线段AB的两个端点A、B分别在x轴和y轴上滑动,点P在线段AB上,且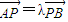 (λ为常数且λ>0).
(λ为常数且λ>0).(I)求点P的轨迹方程C,并说明轨迹类型;
(II)当λ=2时,已知直线l1与原点O的距离为
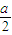 ,且直线l1与轨迹C有公共点,求直线l1的斜率k的取值范围.
,且直线l1与轨迹C有公共点,求直线l1的斜率k的取值范围.
【答案】分析:(I)欲求点P的轨迹方程,设点P(x,y),只须求出其坐标x,y的关系式即可,由题意知点P满足于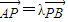 得到一个关系式,再结合线段AB的长度为a(a>0)化简即得点P的轨迹方程,最后对参数λ进行讨论来判断轨迹是什么图形即可.
得到一个关系式,再结合线段AB的长度为a(a>0)化简即得点P的轨迹方程,最后对参数λ进行讨论来判断轨迹是什么图形即可.
(II)设直线l1的方程:y=kx+h,先由直线l1与原点O的距离为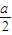 ,得出h与k的关系,再将直线方程代入(1)中的方程,利用根的判别式△=9(4+k2)a2-81h2≥0即可求出斜率k的取值范围.
,得出h与k的关系,再将直线方程代入(1)中的方程,利用根的判别式△=9(4+k2)a2-81h2≥0即可求出斜率k的取值范围.
解答:解:(I)设P(x,y)、A(x,0)、B(0,y),
则 ,
,
由此及|AB|=a⇒x2+y2=a2,得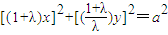 ,
,
即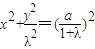 .(*)(3分)
.(*)(3分)
①当0<λ<1时,方程(*)的轨迹是焦点为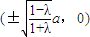 ,
,
长轴长为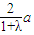 的椭圆;
的椭圆;
②当λ>1时,方程(*)的轨迹是焦点为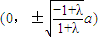 ,
,
长轴长为 的椭圆;
的椭圆;
③当λ=1时,方程(*)的轨迹是焦点为以O点为圆心,
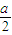 为半径的圆. (6分)
为半径的圆. (6分)
(II)设直线l1的方程:y=kx+h,
据题意有 ,即
,即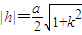 . (9分)
. (9分)
由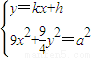
得 .
.
因为直线l1与椭圆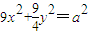 有公共点,
有公共点,
所以△=9(4+k2)a2-81h2≥0,又把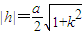 代入上式,
代入上式,
得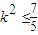 ,∴
,∴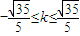 . (12分)
. (12分)
点评:本小题主要考查曲线与方程,直线和圆锥曲线等基础知识,以及求动点轨迹的基本技能和综合运用数学知识解决问题的能力.
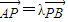 得到一个关系式,再结合线段AB的长度为a(a>0)化简即得点P的轨迹方程,最后对参数λ进行讨论来判断轨迹是什么图形即可.
得到一个关系式,再结合线段AB的长度为a(a>0)化简即得点P的轨迹方程,最后对参数λ进行讨论来判断轨迹是什么图形即可.(II)设直线l1的方程:y=kx+h,先由直线l1与原点O的距离为
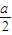 ,得出h与k的关系,再将直线方程代入(1)中的方程,利用根的判别式△=9(4+k2)a2-81h2≥0即可求出斜率k的取值范围.
,得出h与k的关系,再将直线方程代入(1)中的方程,利用根的判别式△=9(4+k2)a2-81h2≥0即可求出斜率k的取值范围.解答:解:(I)设P(x,y)、A(x,0)、B(0,y),
则
 ,
,由此及|AB|=a⇒x2+y2=a2,得
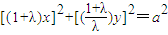 ,
,即
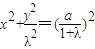 .(*)(3分)
.(*)(3分)①当0<λ<1时,方程(*)的轨迹是焦点为
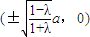 ,
,长轴长为
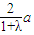 的椭圆;
的椭圆;②当λ>1时,方程(*)的轨迹是焦点为
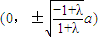 ,
,长轴长为
 的椭圆;
的椭圆;③当λ=1时,方程(*)的轨迹是焦点为以O点为圆心,
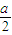 为半径的圆. (6分)
为半径的圆. (6分)(II)设直线l1的方程:y=kx+h,
据题意有
 ,即
,即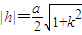 . (9分)
. (9分)由
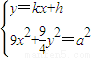
得
 .
.因为直线l1与椭圆
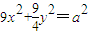 有公共点,
有公共点,所以△=9(4+k2)a2-81h2≥0,又把
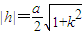 代入上式,
代入上式,得
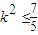 ,∴
,∴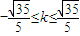 . (12分)
. (12分)点评:本小题主要考查曲线与方程,直线和圆锥曲线等基础知识,以及求动点轨迹的基本技能和综合运用数学知识解决问题的能力.

练习册系列答案
相关题目
 (λ为常数且λ>0).
(λ为常数且λ>0). (λ为常数且λ>0).
(λ为常数且λ>0). ,且直线l1与轨迹C有公共点,求直线l1的斜率k的取值范围.
,且直线l1与轨迹C有公共点,求直线l1的斜率k的取值范围.