题目内容
f(x)
是定义在R上的函数,且对任意x,y都有f(x+y)=f(x)+f(y)-1成立.当x>0时,f(x)>1.(1)证明:f(x)
在R上是增函数;(2)
若f(4)=5,求f(2)的值;(3)
若f(4)=5,解不等式 .
.
答案:略
解析:
解析:
|
(1) 由f(x+y)=f(x)+f(y)-1有 f(x+y)-f(x)=f(y)-1.任取 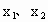 使 使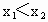 ,则 ,则
由于当 即 ∴故f(x)在R上的增函数. (2) 由f(4)=5,故f(4)=f(2+2)-1=2f(2)-1=5,∴ f(2)=3(3) 由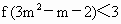 ,故 ,故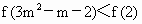 , ,
∵ f(x)在R上是增函数,于是 , ,
解得, 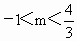 . . |

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
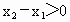 ,于是
,于是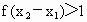 ,
,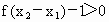 ,∴
,∴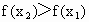 ,
, ,又当-3≤x≤-2时,f(x)=2x,则f(113.5)的值是( )
,又当-3≤x≤-2时,f(x)=2x,则f(113.5)的值是( ) B.
-
B.
- D.
-
D.
-