题目内容
若关于x的不等式(m+1)x2-mx+m-1>0的解集为∅,则实数m的取值范围是
(-∞,-
]
2
| ||
| 3 |
(-∞,-
]
.2
| ||
| 3 |
分析:关于x的不等式(m+1)x2-mx+m-1>0的解集为∅,可转化成不等式(m+1)x2-mx+m-1≤0恒成立,然后讨论二次项系数和判别式可得结论.
解答:解:∵关于x的不等式(m+1)x2-mx+m-1>0的解集为∅,
∴不等式(m+1)x2-mx+m-1≤0恒成立
①当m+1=0时,(m+1)x2-mx+m-1≤0,即x≤2,不是对任意x∈R恒成立;
②当m+1≠0时,?x∈R,使(m+1)x2-mx+m-1≤0,
即m+1<0且△=(-m)2-4(m+1)(m-1)≤0,
化简得:3m2≥4,解得m≥
或m≤-
,
∴m≤-
综上,实数m的取值范围是m≤-
.
故答案为:(-∞,-
].
∴不等式(m+1)x2-mx+m-1≤0恒成立
①当m+1=0时,(m+1)x2-mx+m-1≤0,即x≤2,不是对任意x∈R恒成立;
②当m+1≠0时,?x∈R,使(m+1)x2-mx+m-1≤0,
即m+1<0且△=(-m)2-4(m+1)(m-1)≤0,
化简得:3m2≥4,解得m≥
2
| ||
| 3 |
2
| ||
| 3 |
∴m≤-
2
| ||
| 3 |
综上,实数m的取值范围是m≤-
2
| ||
| 3 |
故答案为:(-∞,-
2
| ||
| 3 |
点评:本题主要考查了二次函数恒成立问题,即根据二次函数图象开口方向和判别式的符号,列出等价条件求出对应的参数的范围,属于基础题.

练习册系列答案
相关题目
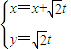 (t为参数).若圆C被直线l平分,则实数x的值为 .
(t为参数).若圆C被直线l平分,则实数x的值为 .