题目内容
若关于x的不等式(m-3)x2-2mx-8>0(m∈R)的解集是一个开区间D,定义开区间(a,b)的长度l=b-a.
(1)求开区间D的长度l(l用m表示),并写出其定义域
(2)若l∈[1,2],求实数m的取值范围.
(1)求开区间D的长度l(l用m表示),并写出其定义域
(2)若l∈[1,2],求实数m的取值范围.
分析:(1)设(m-3)x2-2mx-8=0的两根为x1,x2,根据题意得△=4(m2+8m-24)>0,利用职权根与系数的关系写出两根的和,积,最后利用l的长度公式即可求得开区间D的长度l,结合方程有根条件即可求得其定义域;
(2)结合(1)m的范围及条件:“l∈[1,2],”解关系m的不等关系式,即可得出m的取值范围.
(2)结合(1)m的范围及条件:“l∈[1,2],”解关系m的不等关系式,即可得出m的取值范围.
解答:解:(1)根据题意得m-3<0,设(m-3)x2-2mx-8=0的两根为x1,x2,
则△=4(m2+8m-24)>0,x1+x2=
,x1x2=-
l=|x1-x2|=
=
=
由
⇒m<-4-2
或3>m>-4+2
,
∴函数定义域为(-∞,-4-2
)∪(-4+2
,3)
(2)1≤l=
≤2?(m-3)2≤4(m2+8m-24)≤4(m-3)2?
?
结合(1)m的范围,m的取值范围为(-∞,-15]∪[
,
]
则△=4(m2+8m-24)>0,x1+x2=
| 2m |
| m-3 |
| 8 |
| m-3 |
| (x1+x2)2-4x1x |
(
|
=
2
| ||
| |m-3| |
由
|
| 10 |
| 10 |
∴函数定义域为(-∞,-4-2
| 10 |
| 10 |
(2)1≤l=
2
| ||
| |m-3| |
|
|
结合(1)m的范围,m的取值范围为(-∞,-15]∪[
| 7 |
| 3 |
| 33 |
| 14 |
点评:本小题主要考查一元二次不等式的解法、根式不等式的解法等基础知识,考查运算求解能力与转化思想.属于基础题.

练习册系列答案
相关题目
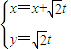 (t为参数).若圆C被直线l平分,则实数x的值为 .
(t为参数).若圆C被直线l平分,则实数x的值为 .