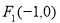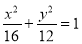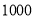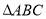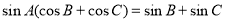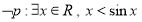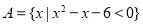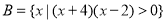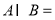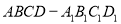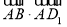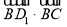题目内容
已知命题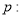 方程
方程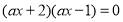 在
在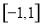 上有解;命题
上有解;命题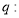 不等式
不等式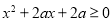 恒成立,若命题“
恒成立,若命题“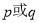 ”是假命题,求
”是假命题,求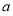 的取值范围.
的取值范围.
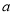 的取值范围是
的取值范围是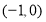 .
.
【解析】
试题分析:先考虑命题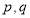 为真时
为真时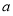 的取值范围,对于
的取值范围,对于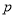 真时,易知
真时,易知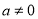 ,于是得到
,于是得到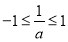 或
或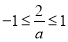 ,求解可得
,求解可得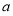 的取值范围;对于
的取值范围;对于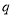 真时,可知
真时,可知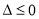 ,求解得到
,求解得到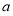 的取值范围;然后根据复合命题的真值表,由命题“
的取值范围;然后根据复合命题的真值表,由命题“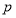 或
或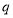 ”是假命题可知
”是假命题可知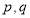 都为假,根据
都为假,根据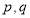 为真时
为真时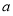 的取值范围得到
的取值范围得到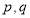 为假时
为假时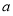 的取值范围,取交集即可.
的取值范围,取交集即可.
试题解析:若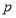 正确,易知
正确,易知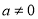
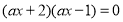 的解为
的解为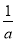 或
或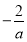 2分
2分
若方程在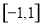 上有解,只需满足
上有解,只需满足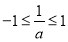 或
或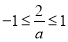 4分
4分
即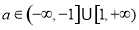 6分
6分
若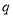 正确,即不等式
正确,即不等式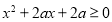 恒成立,则有
恒成立,则有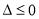 即
即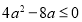
得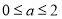 9分
9分
若“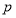 或
或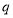 ”是假命题,则
”是假命题,则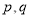 都是假命题
都是假命题
有 12分
12分
所以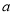 的取值范围是
的取值范围是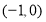 13分.
13分.
考点:1.二次不等式;2.逻辑联结词;3.命题真假的判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目