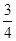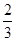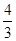题目内容
若等差数列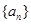 满足:
满足: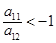 ,且公差
,且公差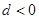 ,其前
,其前 项和为
项和为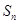 .则满足
.则满足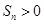 的
的 的最大值为( )
的最大值为( )
| A.11 | B.22 | C.19 | D.20 |
B
解析试题分析:因为公差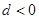 ,且
,且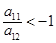 ,所以
,所以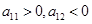 所以
所以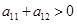 ,所以
,所以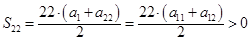 ,又
,又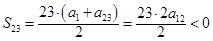 ,所以满足
,所以满足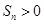 的
的 的最大值为22.
的最大值为22.
考点:等差数列的性质;等差数列前n项和的有关性质。
点评:对于等差数列的前n项和公式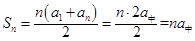 。我们要熟练掌握这条的灵活应用。
。我们要熟练掌握这条的灵活应用。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在等差数列 中,2a4+a7=3,则数列
中,2a4+a7=3,则数列 的前9项和等于( )
的前9项和等于( )
| A.9 | B.6 | C.3 | D.12 |
如果等差数列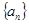 中,
中,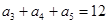 ,那么
,那么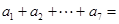 ( )
( )
| A.14 | B.21 | C.28 | D.35 |
已知等差数列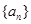 中,
中,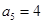 ,前9项和
,前9项和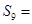 ( )
( )
| A.108 | B.72 | C.36 | D.18 |
等差数列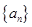 的前
的前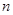 项和为
项和为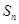 ,已知
,已知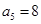 ,
,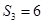 ,则
,则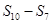 的值是( )
的值是( )
| A.24 | B.48 | C.60 | D.72 |
设Sn是等差数列{an}的前n项和,若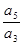 =
=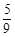 ,则
,则 = ( ).
= ( ).
| A.1 | B.-1 | C.2 | D.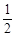 |
在等差数列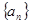 中,
中,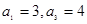 则
则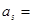 ( )
( )
A. | B.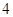 | C.5 | D.-1 |
直线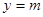 与
与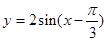 的图像在
的图像在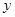 轴右侧从左至右的第
轴右侧从左至右的第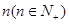 个交点的横坐标记为
个交点的横坐标记为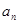 ,若数列
,若数列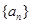 为等差数列,则
为等差数列,则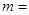 ( )
( )
A.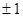 | B.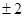 | C.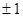 或 或 | D. 或 或 |