题目内容
【题目】已知函数
，
.
（1）若
，当
时，证明：
；
（2）若当
时，
，求
的取值范围.
【答案】（1）证明见解析；（2）
.
【解析】
（1）由
，可得
.令
，利用导数求出函数的单调性求出函数
的最小值为
，可得
，所以
在
上单调递增，据此即可证明结果.
（2）
.令
，
，可得
.令
，
，
，
，所以
在
上单调递增，
所以
，即
，对
进行分类讨论，根据函数的性质即可求出结果.
（1），
，
，.
令，
.
当
时，
，单调递减，
当
时，
，单调递增，
的最小值为，所以
，即，
所以在上单调递增，所以
，故
.
（2）.
令，，
.
令，，，，所以在上单调递增，
所以，即.
①当
，即
时，
，
在
上单调递增，所以
满足条件.
②当
，即
时，
，显然不满足条件.
③当
，即
时，若，
，
令
，，
，
，
故存在
，使
时，
，即
在
上单调递减，所以
，
即，
，故不满足条件.
综上，的取值范围是.
练习册系列答案
相关题目
【题目】2020年3月22日是第二十八届“世界水日”3月22-28日是第三十三届“中国水周”，主题为“坚持节水优先，建设幸福河湖”，效仿阶梯电价，某市准备实施阶梯水价.阶梯水价原则上以一套住宅（一套住宅为一户）的月用水量为基准，具体划分阶梯如下：
梯类 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用水量范围（立方米） |
|
|
|
从本市居民用户中随机抽取10户，并统计了在同一个月份的月用水量，得到如图所示的茎叶图
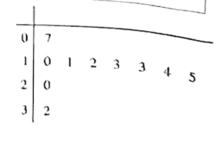
（1）若从这10户中任意抽取三户，求取到第二阶梯用户数
的分布列和数学期望；
（2）用以上样本估计全市的居民用水情况，现从全市随机抽取10户，则抽到多少户为第二阶梯用户的可能性最大？
