题目内容
已知函数f(x)是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足: 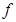 (ab)= a
(ab)= a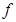 (b)+b
(b)+b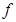 (a),
(a), 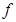 (2)="2," an=
(2)="2," an=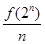 (n∈N*), bn=
(n∈N*), bn=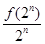 (n∈N*).
(n∈N*).
考察下列结论: ①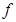 (0)=
(0)= 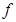 (1); ②
(1); ②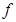 (x)为偶函数; ③数列{an}为等比数列; ④数列{bn}为等差数列.其中正确的结论共有( )
(x)为偶函数; ③数列{an}为等比数列; ④数列{bn}为等差数列.其中正确的结论共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
C
解析试题分析:令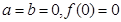 ,再令
,再令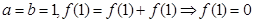 ,所以有
,所以有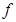 (0)=
(0)= 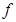 (1)知①正确;令
(1)知①正确;令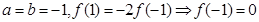 ,从而令
,从而令 故知
故知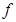 (x)为奇函数,故知②错误;对于③,由于
(x)为奇函数,故知②错误;对于③,由于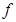 (2)=2,所以
(2)=2,所以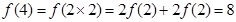 ;从而
;从而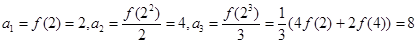 ,猜想
,猜想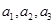 …,成等比数列且
…,成等比数列且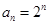 ,用数学归纳法可证明此结论:对于n=1时,猜想显然成立;假设当
,用数学归纳法可证明此结论:对于n=1时,猜想显然成立;假设当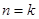 时,猜想正确,即
时,猜想正确,即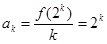 ,从而
,从而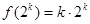 ,那么当
,那么当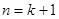 时,
时,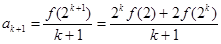
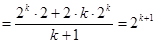 这就是说当
这就是说当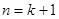 时猜想也成立,故
时猜想也成立,故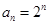 ,故③正确;对于④,因为
,故③正确;对于④,因为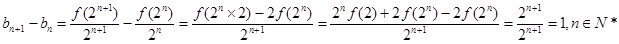 ,所以数列{bn}为等差数列,故④正确.由此可知①③④正确,故选C.
,所以数列{bn}为等差数列,故④正确.由此可知①③④正确,故选C.
考点:1.函数的性质;2.等差数列与等比数列.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
在等差数列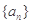 中,
中,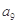 =
=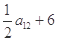 ,则数列
,则数列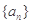 的前11项和
的前11项和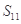 =( )
=( )
| A.24 | B.48 | C.66 | D.132 |
已知等差数列 的首项
的首项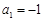 ,公差
,公差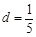 ,则
,则 的第一个正数项是( )
的第一个正数项是( )
A.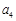 | B.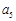 | C.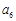 | D.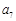 |
若{an}为等差数列,Sn为其前n项和,若首项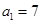 ,公差
,公差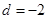 ,则使Sn最大的序号n为( )
,则使Sn最大的序号n为( )
| A.2 | B.3 | C.4 | D.5 |
已知数列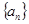 为等差数列,若
为等差数列,若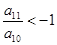 ,且它们的前n项和
,且它们的前n项和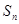 有最大值,
有最大值,
则使得 的n的最大值为( ).
的n的最大值为( ).
| A.11 | B.19 | C.20 | D.21 |
已知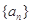 为等差数列,若
为等差数列,若 ,则
,则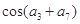 的值为( ).
的值为( ).
A.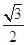 | B.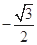 | C.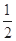 | D.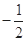 |
设Sn为等差数列{an}的前n项和,若a1=1,公差d=2,Sk+2-Sk=24,则k等于( )
| A.8 | B.7 | C.6 | D.5 |
数列{an}中,a2=2,a6=0且数列{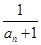 }是等差数列,则a4=( )
}是等差数列,则a4=( )
A.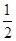 | B.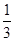 | C.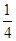 | D.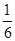 |
[2014·天津市模拟]若等差数列{an}的前5项和S5=25,且a2=3,则a7=( )
| A.12 | B.13 | C.14 | D.15 |