题目内容
已知正四棱锥的底面边长为2,侧棱长为
,则侧面与底面所成的二面角为
| 5 |
60°
60°
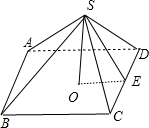
.分析:过S作SO⊥平面ABCD,垂足为O,则O为ABCD的中心,取CD中点E,连接OE,则OE⊥CD,易证∠SEO为侧面与底面所成二面角的平面角,通过解直角三角形可得答案.
解答:解:过S作SO⊥平面ABCD,垂足为O,则O为ABCD的中心,取CD中点E,连接OE,则OE⊥CD,
由三垂线定理知CD⊥SE,
所以∠SEO为侧面与底面所成二面角的平面角,
在Rt△SOE中,SE=
=
=2,OE=1,
所以cos∠SEO=
,则∠SEO=60°,
故答案为:60°.
由三垂线定理知CD⊥SE,
所以∠SEO为侧面与底面所成二面角的平面角,

在Rt△SOE中,SE=
| SD2-ED2 |
| 5-1 |
所以cos∠SEO=
| 1 |
| 2 |
故答案为:60°.
点评:本题考查二面角的平面角及其求法,考查学生推理论证能力,属中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 已知正四棱锥的底面边长为2a,其左视图如图所示.当主视图的面积最大时,该四棱锥的体积和表面积分别为( )
已知正四棱锥的底面边长为2a,其左视图如图所示.当主视图的面积最大时,该四棱锥的体积和表面积分别为( )