题目内容
已知正四棱锥的底面边长为2
，高为3，则侧面与底面所成的二面角等于
．
| 3 |
| π |
| 3 |
| π |
| 3 |
分析：欲求侧面与底面所成的二面角的大小，先找到二面角的平面角，根据二面角的平面角的定义，在二面角的棱上取一点，过这点在二面角的两个面内分别作与棱垂直的射线，这两条射线所成角即二面角的平面角，在正四棱锥中，利用三垂线定理可知，侧面的斜高，底面的弦心距所成角恰好为所求二面角的平面角，再放入直角三角形中，即可解出该角．
解答：解：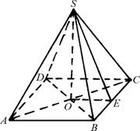
如图，过正四棱锥的顶点S向底面作垂线，垂足为O，
过O向底边BC作垂线，垂足为E，连接SE，
根据三垂线定理，SE⊥BC
∴∠SEO为侧面SBC与底面ABCD所成二面角的平面角
在RT△SOD中，SO=3，OE=
，∴tan∠SEO=
=
=
∴∠SEO=
，即侧面与底面所成的二面角等于
故答案为
如图，过正四棱锥的顶点S向底面作垂线，垂足为O，过O向底边BC作垂线，垂足为E，连接SE，
根据三垂线定理，SE⊥BC
∴∠SEO为侧面SBC与底面ABCD所成二面角的平面角
在RT△SOD中，SO=3，OE=
| 3 |
| |SO| |
| |OD| |
| 3 | ||
|
| 3 |
∴∠SEO=
| π |
| 3 |
| π |
| 3 |
故答案为
| π |
| 3 |
点评：本题主要考查了二面角的大小，解题关键再与找到二面角的平面角．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
已知正四棱锥的底面边长为2a，其左视图如图所示．当主视图的面积最大时，该四棱锥的体积和表面积分别为（ ）