题目内容
某厂生产A产品的年固定成本为250万元,若A产品的年产量为x万件,则需另投入成本C(x)(万元).已知A产品年产量不超过80万件时,C(x)= x2+10x;A产品年产量大于80万件时,C(x)=51x+
x2+10x;A产品年产量大于80万件时,C(x)=51x+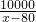 -1450.因设备限制,A产品年产量不超过200万件.现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完.设该厂生产A产品的年利润为L(万元).
-1450.因设备限制,A产品年产量不超过200万件.现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完.设该厂生产A产品的年利润为L(万元).
(1)写出L关于x的函数解析式L(x);
(2)当年产量为多少时,该厂生产A产品所获的利润最大?
解:(1)由题意知
L(x)=50x-C(x)-250=
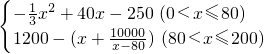 ;
;
(2)①当0<x≤80时,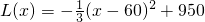 ,所以
,所以
当x=60时,L(x)max=L(60)=950;
②当80<x≤200时,
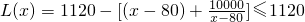
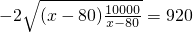 .
.
当且仅当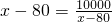 ,即x=180时,“=”成立.
,即x=180时,“=”成立.
因为180∈(80,200],所以L(x)max=920<950.
答:当年产量为60万件时,该厂所获利润最大.
分析:(1)利润L(x)等于销售收入减去固定成本再减去投入成本C(x),根据产量的范围列出分段函数解析式;
(2)当0<x≤80时,利用配方法求二次函数的最值,当80<x≤200时,利用基本不等式求最值.
点评:本题考查了函数模型的选择及应用,考查了分段函数的值域的求法,训练了利用配方法求二次函数的最值及利用基本不等式求最值,是中档题.
L(x)=50x-C(x)-250=
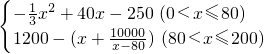 ;
;(2)①当0<x≤80时,
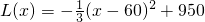 ,所以
,所以当x=60时,L(x)max=L(60)=950;
②当80<x≤200时,
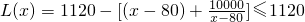
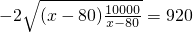 .
.当且仅当
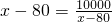 ,即x=180时,“=”成立.
,即x=180时,“=”成立.因为180∈(80,200],所以L(x)max=920<950.
答:当年产量为60万件时,该厂所获利润最大.
分析:(1)利润L(x)等于销售收入减去固定成本再减去投入成本C(x),根据产量的范围列出分段函数解析式;
(2)当0<x≤80时,利用配方法求二次函数的最值,当80<x≤200时,利用基本不等式求最值.
点评:本题考查了函数模型的选择及应用,考查了分段函数的值域的求法,训练了利用配方法求二次函数的最值及利用基本不等式求最值,是中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
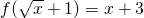 ,则f(x+1)的解析式为
,则f(x+1)的解析式为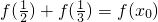 ,求x0的值;
,求x0的值;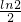 ,
, ,c=
,c=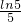 ,则
,则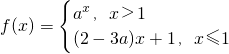 是R上的减函数,则实数a的取值范围是
是R上的减函数,则实数a的取值范围是
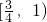
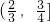

 在(0,+∞)上都是减函数,则函数f(x)=bx+a在R上是
在(0,+∞)上都是减函数,则函数f(x)=bx+a在R上是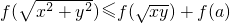 恒成立,则实数a的取值范围是________.
恒成立,则实数a的取值范围是________.