题目内容
若点P、Q分别在函数y=ex和函数 y=lnx的图象上,则P、Q两点间的距离的最小值是 .
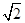
试题分析:考虑到两曲线关于直线y=x对称,求丨PQ丨的最小值可转化为求P到直线y=x的最小距离,再利用导数的几何意义,求曲线上斜率为1的切线方程,从而得此距离。解:∵曲线y=ex与曲线y=lnx互为反函数,其图象关于y=x对称,故可先求点P到直线y=x的最近距离d,设曲线y=ex上斜率为1的切线为y=x+b,∵y’=ex,由ex=1,得x=0,故切点坐标为(0,1),即b=1
 ,∴丨PQ丨的最小值为2d=2
,∴丨PQ丨的最小值为2d=2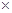

点评:本题主要考查了互为反函数的函数图象的对称性,以及导数的几何意义,曲线的切线方程的求法,同时考查了化归的思想方法,属于中档题

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 的图象与
的图象与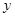 轴相交于点
轴相交于点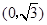 ,且该函数的最小正周期为
,且该函数的最小正周期为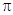 .
.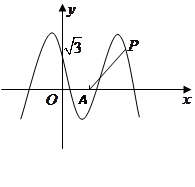
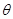 和
和 的值;
的值;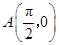 ,点
,点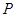 是该函数图象上一点,
是该函数图象上一点,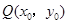 是
是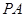 的中点,当
的中点,当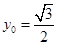 ,
,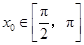 时,求
时,求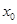 的值.
的值. 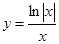 的图象大致是 ( )
的图象大致是 ( )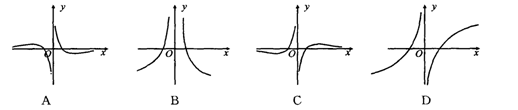
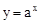 (a>0且a≠1)与函数y=(1-a)x的图象只能是( )
(a>0且a≠1)与函数y=(1-a)x的图象只能是( )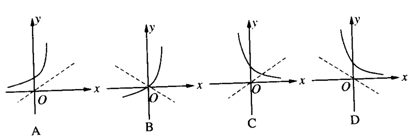
 的图像,则下列命题错误的是( )
的图像,则下列命题错误的是( )
 处有极小值
处有极小值  处有极大值
处有极大值 处有极小值
处有极小值  处有极小值
处有极小值 的图象
的图象 对称
对称 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 取值范围是( )
取值范围是( ) 与
与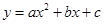 的图象关系可能正确的是( )
的图象关系可能正确的是( )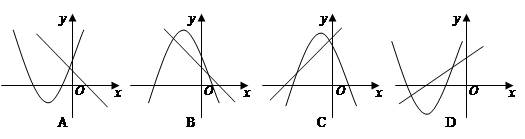
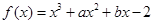 的图象过点
的图象过点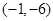 ,且函数
,且函数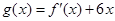 的图象关于
的图象关于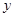 轴对称;
轴对称;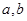 的值及函数
的值及函数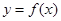 的单调区间;
的单调区间;