题目内容
下列叙述中其中正确的序号为:
①函数y=tanx是单调递增函数.
②函数y=x+
是奇函数,在区间(1,+∞)上是增函数.
③函数y=sinx+cosx的最大值是2.
④二次函数y=ax2+bx+c是偶函数的条件是b=0.
②④
②④
.①函数y=tanx是单调递增函数.
②函数y=x+
| 1 | x |
③函数y=sinx+cosx的最大值是2.
④二次函数y=ax2+bx+c是偶函数的条件是b=0.
分析:根据正切函数的性质判断①中函数y=tanx进行判断即可;利用奇偶性的定义看f(-x)和f(x)的关系易判断函数y=x+
是奇函数,利用导数易得它的单调增区间是(1,+∞);③可以化为y=Asin(ωx+φ)形式,结合正弦函数的图象求最值;④题目条件:“二次函数y=ax2+bx+c(a≠0)是偶函数,”根据二次函数的对称性,得其对称轴是y轴,从而求得b.
| 1 |
| x |
解答:解:对于①函数y=tanx在定义域内为增函数;在每一个单调区间是增函数,定义域内不是增函数.故错;
②中y=x+
,所以f(-x)=-f(-x),为奇函数,而y′=1-
>0,得x<-1或x>1,函数y=x+
在区间(1,+∞)上是增函数,故②正确;
③函数y=sinx+cosx=
sin(x+
)∈[-
,
],有最大值
,故③错误;
④由题意,得二次函数的图象关于y轴对称,则对称轴为x=-
=0,则b=0,故④正确.
故答案为:②④.
②中y=x+
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
③函数y=sinx+cosx=
| 2 |
| π |
| 4 |
| 2 |
| 2 |
| 2 |
④由题意,得二次函数的图象关于y轴对称,则对称轴为x=-
| b |
| 2a |
故答案为:②④.
点评:本题考查函数的值域、单调性和奇偶性等性质,是基础知识、基本题型的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
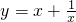 是奇函数,在区间(1,+∞)上是增函数.
是奇函数,在区间(1,+∞)上是增函数.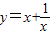 是奇函数,在区间(1,+∞)上是增函数.
是奇函数,在区间(1,+∞)上是增函数.