题目内容
已知a>0,函数f(x)=lnx-ax2,x>0.(f(x)的图象连续不断)
(Ⅰ)当a=
时
①求f(x)的单调区间;
②证明:存在x0∈(2,+∞),使f(x0)=f(
);
(Ⅱ)若存在均属于区间[1,3]的α,β,且β-α≥1,使f(α)=f(β),证明
≤a≤
.
(Ⅰ)当a=
| 1 |
| 8 |
①求f(x)的单调区间;
②证明:存在x0∈(2,+∞),使f(x0)=f(
| 3 |
| 2 |
(Ⅱ)若存在均属于区间[1,3]的α,β,且β-α≥1,使f(α)=f(β),证明
| ln3-ln2 |
| 5 |
| ln2 |
| 3 |
分析:(I)将a=
代入可得函数的解析式,
①求导数fˊ(x);在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0确定的单调区间
②由(I)知f(x)在(0,2)内单调递增,在(2,+∞)内单调递减.令g(x)=f(x)-f(
).利用函数f(x)在(0,2)内单调递增,得到f(2)>f(
),即g(2)>0.最后取x′=
e>2,则g(x′)=
<0.从而得到结论;
(II)先由f(α)=f(β)及(I)的结论知α<
<β,从而f(x)在[α,β]上的最小值为f(a).再依1≤α≤2≤β≤3建立关于a的不等关系即可证得结论.
| 1 |
| 8 |
①求导数fˊ(x);在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0确定的单调区间
②由(I)知f(x)在(0,2)内单调递增,在(2,+∞)内单调递减.令g(x)=f(x)-f(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 41-9e2 |
| 32 |
(II)先由f(α)=f(β)及(I)的结论知α<
| ||
| 2a |
解答:解:(I)①当a=
时,f(x)=lnx-
x2.
∴f′(x)=
-
x=
,x∈(0,+∞),
令f′(x)=0,解得x=2.
当x变化时,f'(x),f(x)的变化情况如下表:
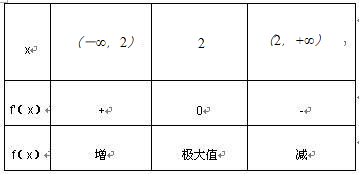
所以,f(x)的单调递增区间是(0,
),f(x)的单调递减区间是(
,+∞).
证明:②由(I)知f(x)在(0,2)内单调递增,在(2,+∞)内单调递减.
令g(x)=f(x)-f(
).
由于f(x)在(0,2)内单调递增,
故f(2)>f(
),即g(2)>0.
取x′=
e>2,则g(x′)=
<0.
所以存在x0∈(2,x'),使g(x0)=0,
即存在x0∈(2,+∞),使f(x0)=f(
).
(II)证明:由f(α)=f(β)及(I)的结论知α<
<β,
从而f(x)在[α,β]上的最小值为f(a).
又由β-α≥1,α,β∈[1,3],知1≤α≤2≤β≤3.
故
即
从而
≤a≤
.
| 1 |
| 8 |
| 1 |
| 8 |
∴f′(x)=
| 1 |
| x |
| 1 |
| 4 |
1-
| ||
| x |
令f′(x)=0,解得x=2.
当x变化时,f'(x),f(x)的变化情况如下表:

所以,f(x)的单调递增区间是(0,
| ||
| 2a |
| ||
| 2a |
证明:②由(I)知f(x)在(0,2)内单调递增,在(2,+∞)内单调递减.
令g(x)=f(x)-f(
| 3 |
| 2 |
由于f(x)在(0,2)内单调递增,
故f(2)>f(
| 3 |
| 2 |
取x′=
| 3 |
| 2 |
| 41-9e2 |
| 32 |
所以存在x0∈(2,x'),使g(x0)=0,
即存在x0∈(2,+∞),使f(x0)=f(
| 3 |
| 2 |
(II)证明:由f(α)=f(β)及(I)的结论知α<
| ||
| 2a |
从而f(x)在[α,β]上的最小值为f(a).
又由β-α≥1,α,β∈[1,3],知1≤α≤2≤β≤3.
故
|
即
|
从而
| ln3-ln2 |
| 5 |
| ln2 |
| 3 |
点评:本小题主要考查导数的运算、利用导数研究函数的单调性、解不等式、函数的零点等基础知识,考查运算能力和运用函数思想分析解决问题的能力及分类讨论的思想方法.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
| A、?x∈R,f(x)≤f(x0) | B、?x∈R,f(x)≥f(x0) | C、?x∈R,f(x)≤f(x0) | D、?x∈R,f(x)≥f(x0) |