题目内容
如图是某简单组合体的三视图,则该组合体的体积为( ) 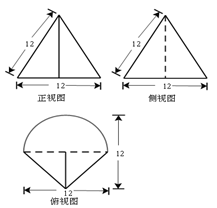
A.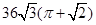 | B.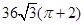 |
C.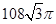 | D.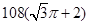 |
B
解析试题分析:由三视图可知几何体是由截面相同的半个圆锥与半个三棱锥组合而成的。圆椎底面半径为 ,椎体底面边长为
,椎体底面边长为 ,高为
,高为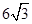 .
. 故选
故选 .
.
考点:本题考查了三视图的运用
点评:由三视图还原空间几何体以及掌握空间几何体的体积和表面积公式是解决此类问题的关键

练习册系列答案
相关题目
已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )
A. | B. | C. | D. |
某空间几何体的三视图及尺寸如图,则该几何体的体积是
A. | B. | C.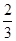 | D.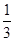 |
已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2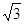 ,AB=1,AC=2,∠BAC=60°,则球O的表面积为
,AB=1,AC=2,∠BAC=60°,则球O的表面积为
A.4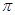 | B.12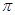 | C.16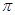 | D.64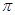 |
下列说法中正确的是
| A.棱柱的侧面可以是三角形 |
| B.正方体和长方体都是特殊的四棱柱 |
| C.所有的几何体的表面都能展成平面图形 |
| D.棱柱的各条棱都相等 |
若三棱锥的三视图如右图所示,则该三棱锥的体积为【 】.
A. | B.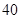 | C.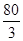 | D. |
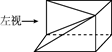
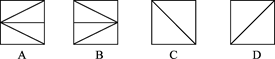
如图是某几何体的三视图,则该几何体的体积为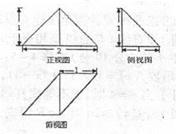
| A.1 | B.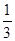 | C. | D.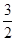 |
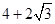 的圆柱形有盖容器中,放入一个半径为3的大球后再放入与球面、圆柱侧面及上底面均相切的小球,则放入的小球的个数最多的为
的圆柱形有盖容器中,放入一个半径为3的大球后再放入与球面、圆柱侧面及上底面均相切的小球,则放入的小球的个数最多的为