题目内容
己知点(2,2)在直线y=kx+b上,且原点到该线的距离为1,求直线的方程.
考点:点到直线的距离公式,直线的斜截式方程
专题:计算题,直线与圆
分析:由点(2,2)在直线y=kx+b上,可得2=2k+b;由原点到该线的距离为1,可得
=1,从而可解得k,b的值,即可求出直线的方程.
| |b| | ||
|
解答:
解:∵点(2,2)在直线y=kx+b上,
∴2=2k+b…①
∵原点到该线的距离为1,
∴
=1,…②
由①②可解得k=
,b=-
±
.
∴直线方程为y=
x-
±
.
∴2=2k+b…①
∵原点到该线的距离为1,
∴
| |b| | ||
|
由①②可解得k=
4±
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
∴直线方程为y=
4±
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
点评:本题主要考察了点到直线的距离公式,直线的斜截式方程,属于基本知识的考查.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
下列命题中正确的是( )
| A、三角形的内角是第一象限角或第二象限角 | ||
| B、第一象限角是锐角 | ||
| C、第一象限角不是锐角 | ||
D、角α是第四象限角则有2kπ-
|
若0<x<
,则2x与3sin x的大小关系( )
| π |
| 2 |
| A、2x>3sin x |
| B、2x<3sin x |
| C、2x=3sin x |
| D、与x的取值有关 |
设抛物线的顶点在原点,准线方程为y=2,则抛物线的方程是( )
| A、x2=8y |
| B、x2=-8y |
| C、y2=-8x |
| D、y2=-8x |
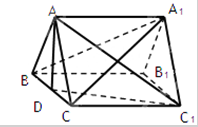 如图所示,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为3,且侧棱AA1⊥面ABC,点D是BC的中点,求证:平面BB1C1C丄平面ADC1.
如图所示,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为3,且侧棱AA1⊥面ABC,点D是BC的中点,求证:平面BB1C1C丄平面ADC1.