题目内容
在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为________.
解析试题分析:如图,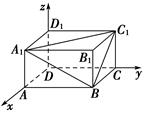
建立空间直角坐标系Dxyz,则D1(0,0,1),C1(0,2,1),A1(1,0,1),B(1,2,0),
∴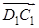 =(0,2,0),设平面A1BC1的一个法向量为n=(x,y,z),由
=(0,2,0),设平面A1BC1的一个法向量为n=(x,y,z),由 令y=1,得
令y=1,得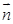 =(2,1,2),
=(2,1,2),
设D1C1与平面A1BC1所成角为θ,则sin θ=|cos〈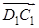 ,n〉|=
,n〉|=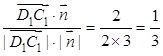 ,即直线D1C1与平面A1BC1所成角的正弦值为
,即直线D1C1与平面A1BC1所成角的正弦值为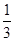 .
.
考点:线面成角.

练习册系列答案
相关题目

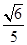
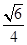
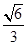
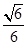

 ,2),则m= .
,2),则m= .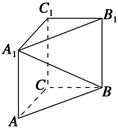
 的棱长为1,点
的棱长为1,点 在侧面
在侧面 及其边界上运动,并且总保持
及其边界上运动,并且总保持 平行平面
平行平面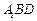 ,则动点P的轨迹的长度是 _______ .
,则动点P的轨迹的长度是 _______ .
