题目内容
已知函数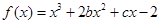 的图象在与
的图象在与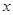 轴交点处的切线方程是
轴交点处的切线方程是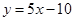 .
.
(I)求函数 的解析式;
的解析式;
(II)设函数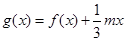 ,若
,若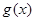 的极值存在,求实数
的极值存在,求实数 的取值范围以及函数
的取值范围以及函数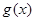 取得极值时对应的自变量
取得极值时对应的自变量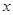 的值.
的值.
(I)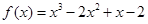 ;(II)
;(II)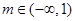 时,函数
时,函数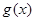 有极值;
有极值;
当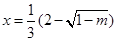 时,
时,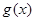 有极大值;当
有极大值;当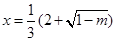 时,
时,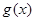 有极小值.
有极小值.
解析试题分析:( I)涉及切线,便要求出切点.本题中切点如何求?函数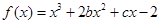 的图象在与
的图象在与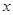 轴交点处的切线方程是
轴交点处的切线方程是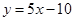 .说明切点就是直线
.说明切点就是直线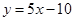 与
与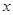 轴交点,所以令
轴交点,所以令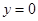 便得切点为(2,0).切点既在切线上又曲线,所以有
便得切点为(2,0).切点既在切线上又曲线,所以有 , 即
, 即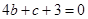 .
.
函数在切点处的导数就是切线的斜率,所以由已知有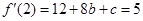 即
即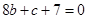 .这样便得一个方程组,解这个方程组求出
.这样便得一个方程组,解这个方程组求出 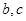 便
便 的解析式.
的解析式.
(II)将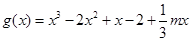 求导得,
求导得,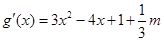 ,
,
令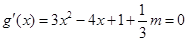 .这是一个二次方程,要使得函数有极值,则方程要有两个不同的实数根,所以
.这是一个二次方程,要使得函数有极值,则方程要有两个不同的实数根,所以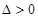 ,由此可得
,由此可得 的范围.解方程
的范围.解方程 有便得取得极值时
有便得取得极值时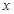 的值.
的值.
试题解析:( I)由已知,切点为(2,0), 故有 , 即
, 即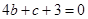
又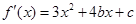 ,由已知
,由已知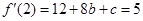 得
得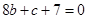
联立①②,解得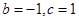 .所以函数的解析式为
.所以函数的解析式为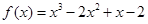
(II)因为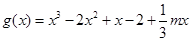
令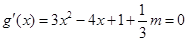
当函数有极值时,则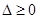 ,方程
,方程 有实数解, 由
有实数解, 由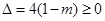 ,得
,得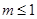 .
.
①当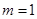 时,
时,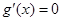 有实数
有实数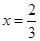 ,在
,在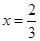 左右两侧均有
左右两侧均有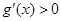 ,故函数
,故函数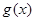 无极值
无极值
②当m<1时,g'(x)=0有两个实数根x1=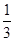 (2
(2 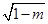 ), x2=
), x2=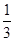 (2+
(2+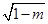 ), g(x),g'(x) 的情况如下表:
), g(x),g'(x) 的情况如下表:
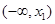
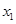
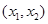
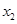
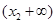
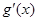


 ,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0. 的解析式;
的解析式;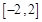 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ,求实数
,求实数 的最小值;
的最小值;
 ,可作曲线
,可作曲线 的三条切线,求实数
的三条切线,求实数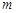 的取值范围.
的取值范围.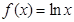 ,
,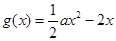 .
.
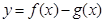 在
在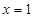 与
与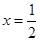 处的切线相互平行,求
处的切线相互平行,求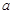 的值及切线斜率;
的值及切线斜率;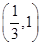 上单调递减,求
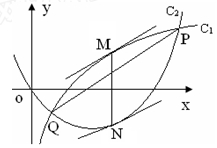
上单调递减,求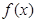 的图像C1与函数
的图像C1与函数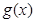 的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.
的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行. ,函数
,函数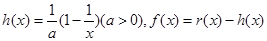 .
.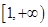 上是单调递增函数,试求实数a的取值范围:
上是单调递增函数,试求实数a的取值范围: 是公差为1.首项为l的等差数列,数列
是公差为1.首项为l的等差数列,数列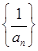 的前n项和为
的前n项和为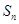 ,求证:当
,求证:当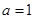 时,
时,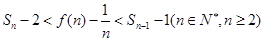 .
.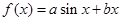 的图像在点
的图像在点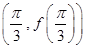 处的切线方程为
处的切线方程为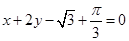 .
. ,
,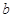 的值;
的值;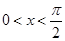 时,
时,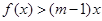 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
,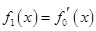 ,
,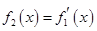 ,
,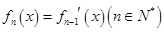 .
.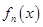 表达式(不需证明);
表达式(不需证明);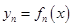 ;
;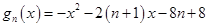 ,
, 的最大值为
的最大值为 ,
,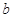 ,试求
,试求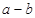 的最小值.
的最小值.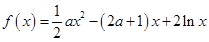 .
. 在
在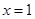 和
和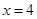 处的切线相互平行,求
处的切线相互平行,求 的值;
的值;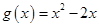 ,对任意的
,对任意的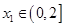 ,均存在
,均存在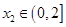 ,使得
,使得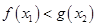 .试求实数
.试求实数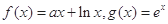 .
.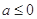 时,求
时,求 的单调区间
的单调区间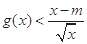 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;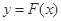 和
和 在其公共定义域内的任意实数
在其公共定义域内的任意实数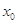 ,称
,称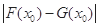 的值为两函数在
的值为两函数在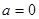 时,函数
时,函数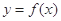 和
和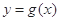 在其公共定义域内的所有差值都大干2。
在其公共定义域内的所有差值都大干2。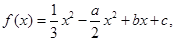 其中
其中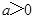 ,曲线
,曲线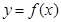 在点
在点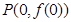 处的切线方程为
处的切线方程为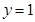 .
.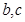 的值;
的值;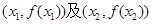 处的切线都过点(0,2).证明:当
处的切线都过点(0,2).证明:当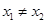 时,
时,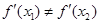 ;
; 的取值范围.
的取值范围.