题目内容
设函数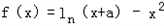 .
.
(1)若a=0,求f(x)在(0,m](m>0)上的最大值g(m).
(2)若f(x)在区间[1,2]上为减函数,求a的取值范围.
(3)若直线y=x为函数f(x)的图象的一条切线,求a的值.
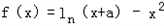 .
.(1)若a=0,求f(x)在(0,m](m>0)上的最大值g(m).
(2)若f(x)在区间[1,2]上为减函数,求a的取值范围.
(3)若直线y=x为函数f(x)的图象的一条切线,求a的值.
解:(1)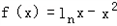 ,x>0,
,x>0,
令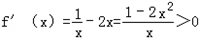 ,
,
∴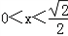 ,
,
∴f(x)在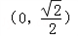 为增函数,
为增函数,
同理可得f(x)在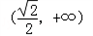 为减函数,
为减函数,
故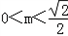 时,f(x)最大值为
时,f(x)最大值为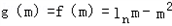 ,
,
当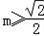 时,f(x)最大值为
时,f(x)最大值为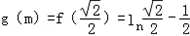 ,
,
综上: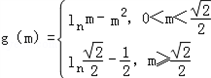 .
.
(2)∵f(x)在[1,2]上为减函数
∴x∈[1,2]有x+a>0恒成立 a>﹣1且
a>﹣1且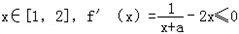 恒成立
恒成立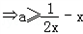 ,而
,而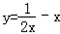 在[1,2为减函数],
在[1,2为减函数],
∴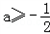 ,又a>﹣1
,又a>﹣1
故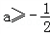 为所求.
为所求.
(3)设切点为P(x0,x0),
则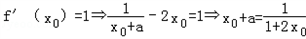 ,
,
且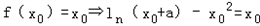 ,
,
∴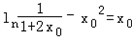 ,即:
,即: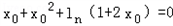 ,
,
再令h(x)=x+x2+ln(1+2x),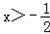 ,
,
∴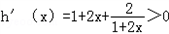 ,
,
∴h(x)在为增函数,又h(0)=0,
∴h(x0)=0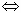 x0=0.
x0=0.
则 a=1为所求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
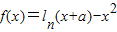 .
.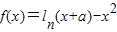 .
.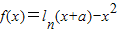 .
. .
.