题目内容
已知向量m=(x2,y-cx),n=(1,x+b)(x,y,b,c∈R)且m∥n,把其中x,y所满足的关系式记为y=f(x).若f′(x)为f(x)的导函数,F(x)=f(x)+af'(x)(a>0),且F(x)是R上的奇函数.
(Ⅰ)求
和c的值;
(Ⅱ)求函数f(x)的单调递减区间(用字母a表示);
(Ⅲ)当a=2时,设0<t<4且t≠2,曲线y=f(x)在点A(t,f(t))处的切线与曲线y=f(x)相交于点B(m,f(m))(A与B不重合),直线x=t与y=f(m)相交于点C,△ABC的面积为S,试用t表示△ABC的面积S(t);并求S(t)的最大值.
(Ⅰ)求
| b |
| a |
(Ⅱ)求函数f(x)的单调递减区间(用字母a表示);
(Ⅲ)当a=2时,设0<t<4且t≠2,曲线y=f(x)在点A(t,f(t))处的切线与曲线y=f(x)相交于点B(m,f(m))(A与B不重合),直线x=t与y=f(m)相交于点C,△ABC的面积为S,试用t表示△ABC的面积S(t);并求S(t)的最大值.
(Ⅰ)∵f(x)=x3+bx2+cx,∴f'(x)=3x2+2bx+c.…(1分)
∵F(x)=f(x)+af'(x)=x3+(b+3a)x2+(c+2ab)x+ac为奇函数,
由F(-x)=-F(x),可得b+3a=0,ac=0.
∵a>0,∴b=-3a,c=0.
∴
=-3,c=0.…(3分)
(Ⅱ)由(Ⅰ)可得f(x)=x3-3ax2,
∴f'(x)=3x(x-2a).
令3x(x-2a)≤0,解得0≤x≤2a.
∴函数f(x)的单调递减区间为[0,2a]
(Ⅲ)当a=2时,曲线y=f(x)在点A(t,f(t))处的切线方程为:
y-f(t)=f'(t)(x-t),
kAB=f'(t)=3t(t-4).
联立方程组
化简,得f(x)-f(t)=f'(t)(x-t).
即x3-6x2-t3+6t2=(3t2-12t)(x-t),(x-t)(x2+xt+t2-6x-6t)=(x-t)(3t2-12t).
∵A、B不重合,∴x≠t.
∴x2+xt+t2-6x-6t=3t2-12t.
∴x2+(t-6)x-2t2+6t=0.
即(x-t)(x+2t-6)=0.
∵x≠t,∴x=-2t+6.
又另一交点为B(m,f(m)),∴m=-2t+6.…(2分)
S(t)=
|m-t|•|f(m)-f(t)|=
(m-t)2•|kAB|=
(t-2)2•3t(4-t)=
(t-2)2(4-t)t,t∈(0,2)∪(2,4).
令h(t)=(t-2)2(4-t)t,其中t∈(0,2)∪(2,4).
∵h(t)=-(t4-8t3+20t2-16t),
∴h'(t)=-4(t3-6t2+10t-4)=-4(t-2)(t-2+
)(t-2-
).
由
解得0<t≤2-
,或2<t≤
.
于是函数h(t)在区间(0,2-
]、(2,2+
]上是单调增函数;
在区间[2-
,2)、[2+
,4)上是单调减函数.
当t=2-
和t=2+
时,函数y=h(t)有极大值.
∴h(t)max=h(2-
)=h(2+
)=4.
∴S(t)max=54.…(3分)
∵F(x)=f(x)+af'(x)=x3+(b+3a)x2+(c+2ab)x+ac为奇函数,
由F(-x)=-F(x),可得b+3a=0,ac=0.
∵a>0,∴b=-3a,c=0.
∴
| b |
| a |
(Ⅱ)由(Ⅰ)可得f(x)=x3-3ax2,
∴f'(x)=3x(x-2a).
令3x(x-2a)≤0,解得0≤x≤2a.
∴函数f(x)的单调递减区间为[0,2a]
(Ⅲ)当a=2时,曲线y=f(x)在点A(t,f(t))处的切线方程为:
y-f(t)=f'(t)(x-t),
kAB=f'(t)=3t(t-4).
联立方程组
|
化简,得f(x)-f(t)=f'(t)(x-t).
即x3-6x2-t3+6t2=(3t2-12t)(x-t),(x-t)(x2+xt+t2-6x-6t)=(x-t)(3t2-12t).
∵A、B不重合,∴x≠t.
∴x2+xt+t2-6x-6t=3t2-12t.
∴x2+(t-6)x-2t2+6t=0.
即(x-t)(x+2t-6)=0.
∵x≠t,∴x=-2t+6.
又另一交点为B(m,f(m)),∴m=-2t+6.…(2分)
S(t)=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |
令h(t)=(t-2)2(4-t)t,其中t∈(0,2)∪(2,4).
∵h(t)=-(t4-8t3+20t2-16t),
∴h'(t)=-4(t3-6t2+10t-4)=-4(t-2)(t-2+
| 2 |
| 2 |
由
|
解得0<t≤2-
| 2 |
| 2 |
于是函数h(t)在区间(0,2-
| 2 |
| 2 |
在区间[2-
| 2 |
| 2 |
当t=2-
| 2 |
| 2 |
∴h(t)max=h(2-
| 2 |
| 2 |
∴S(t)max=54.…(3分)

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
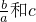 的值;
的值;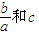 的值;
的值;