题目内容
定义空间两个向量的一种运算
⊕
=|
|-|
|sin＜
，
＞，则关于空间向量上述运算的以下结论中，
①
⊕
=
⊕
，
②λ（
⊕
）=（λ
）⊕
，
③（
⊕
）⊕
=（
⊕
）（
⊕
），
④若
=（x1，y1），
=（x2，y2），则
⊕
=|x1y2-x2y1|；
恒成立的个数有（ ）
| a |
| b |
| a |
| b |
| a |
| b |
①
| a |
| b |
| b |
| a |
②λ（
| a |
| b |
| a |
| b |
③（
| a |
| b |
| c |
| a |
| c |
| b |
| c |
④若
| a |
| b |
| a |
| b |
恒成立的个数有（ ）
分析：①和②需要根据定义列出左边和右边的式子，再验证两边是否恒成立；③由定义知这类：“
⊕
”运算的结果是实数，从而得到结论不成立；④根据数量积求出cos＜
，
＞，再由平方关系求出sin＜
，
＞的值，代入定义进行化简验证即可．
| a |
| b |
| a |
| b |
| a |
| b |
解答：解：①、∵
⊕
=|
|-|
|sin＜
，
＞，
∴
⊕
=|
|-|
|sin＜
，
＞，故
⊕
=
⊕
不会恒成立；
②、∵λ(
⊕
)=λ(|
|-|
|sin＜
，
＞)，且(λ
)⊕
=|λ||
|-|
|sin＜λ
，
＞，
∴λ(
⊕
)=(λ
)⊕
不会恒成立；
③、由定义知
⊕
、
⊕
、
⊕
结果是实数，而
是向量，故（
⊕
）⊕
≠（
⊕
）（
⊕
）；
④、∵cos＜
，
＞=
，∴sin＜
，
＞=
，
∴
⊕
=|
|-|
|×
=|
|-
=
-
≠|x1y2-x2y1|．不成立
综上，恒成立的命题个数为零
故选A．
| a |
| b |
| a |
| b |
| a |
| b |
∴
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
| a |
②、∵λ(
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴λ(
| a |
| b |
| a |
| b |
③、由定义知
| a |
| b |
| a |
| c |
| b |
| c |
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| c |
④、∵cos＜
| a |
| b |
| x1x2+y1y2 | ||||
|
|
| a |
| b |
1-(
|
∴
| a |
| b |
| a |
| b |
1-(
|
| a |
|
|
=
| x12+y12 |
x22+y22-(
|
综上，恒成立的命题个数为零
故选A．
点评：本题考查了向量的数量积和向量的模的公式，利用给出的定义进行证明结论，计算量很大．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
⊕
=|
|-|
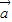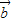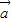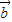|sin＜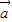
，
＞，则关于空间向量上述运算的以下结论中，
⊕
=
⊕
，
⊕
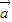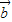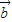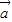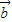）=（λ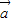
）⊕
，
⊕
）⊕
=（
⊕
）（
⊕
），
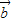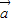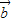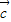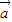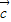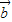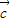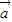=（x1，y1），
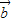=（x2，y2），则
⊕
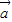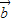=|x1y2-x2y1|；