题目内容
已知二次曲线Ck的方程:
+
=1.
(1)分别求出方程表示椭圆和双曲线的条件;
(2)若双曲线Ck与直线y=x+1有公共点且实轴最长,求双曲线方程;
(3)m、n为正整数,且m<n,是否存在两条曲线Cm、Cn,其交点P与点F1(-
,0),F2(
,0)满足PF1⊥PF2,若存在,求m、n的值;若不存在,说明理由.
| x2 |
| 9-k |
| y2 |
| 4-k |
(1)分别求出方程表示椭圆和双曲线的条件;
(2)若双曲线Ck与直线y=x+1有公共点且实轴最长,求双曲线方程;
(3)m、n为正整数,且m<n,是否存在两条曲线Cm、Cn,其交点P与点F1(-
| 5 |
| 5 |
分析:(1)当且仅当分母都为正,且不相等时,方程表示椭圆;当且仅当分母异号时,方程表示双曲线.
(2)将直线与曲线联立
化简得:(13-2k)x2+2(9-k)x+(9-k)(k-3)=0,利用双曲线Ck与直线y=x+1有公共点,可确定k的范围,从而可求双曲线的实轴,进而可得双曲线方程;
(3)由(1)知C1,C2,C3是椭圆,C5,C6,C7,C8是双曲线,结合图象的几何性质,任意两椭圆之间无公共点,任意两双曲线之间无公共点,从而可求.
(2)将直线与曲线联立
|
(3)由(1)知C1,C2,C3是椭圆,C5,C6,C7,C8是双曲线,结合图象的几何性质,任意两椭圆之间无公共点,任意两双曲线之间无公共点,从而可求.
解答:解:(1)当且仅当
⇒k<4时,方程表示椭圆;----(2分)
当且仅当(9-k)(4-k)<0⇒4<k<9时,方程表示双曲线.---(4分)
(2)
化简得:(13-2k)x2+2(9-k)x+(9-k)(k-3)=0----(6分)
△≥0⇒k≥6或k≤4所以6≤k<9-------(8分)
双曲线的实轴为2
,当k=6时,双曲线实轴最长为2
此时双曲线方程为
-
=1-------(10分)
(3)由(1)知C1,C2,C3是椭圆,C5,C6,C7,C8是双曲线,结合图象的几何性质
任意两椭圆之间无公共点,任意两双曲线之间无公共点------(12分)
设|PF1|=d1,|PF2|=d2,m∈{1,2,3},n∈{5,6,7,8}
由椭圆与双曲线定义及
•
=0;
所以m+n=8-----(16分)
所以这样的Cm,Cn存在,且
或
或
-----(18分)
|
当且仅当(9-k)(4-k)<0⇒4<k<9时,方程表示双曲线.---(4分)
(2)
|
△≥0⇒k≥6或k≤4所以6≤k<9-------(8分)
双曲线的实轴为2
| 9-k |
| 3 |
此时双曲线方程为
| x2 |
| 3 |
| y2 |
| 2 |
(3)由(1)知C1,C2,C3是椭圆,C5,C6,C7,C8是双曲线,结合图象的几何性质
任意两椭圆之间无公共点,任意两双曲线之间无公共点------(12分)
设|PF1|=d1,|PF2|=d2,m∈{1,2,3},n∈{5,6,7,8}
由椭圆与双曲线定义及
| PF1 |
| PF2 |
|
所以这样的Cm,Cn存在,且
|
|
|
点评:本题以二次曲线为载体,考查二次曲线的性质,考查直线与曲线的位置关系,有一定难度.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
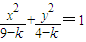 .
.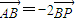 ?若存在,求出k的值;若不存在,说明理由;
?若存在,求出k的值;若不存在,说明理由;