题目内容
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为
、
、p,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为
.
(1)求p的值.
(2)设甲、乙、丙三人中破译出密码的人数为X,求X的分布列和数学期望E(X).
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
(1)求p的值.
(2)设甲、乙、丙三人中破译出密码的人数为X,求X的分布列和数学期望E(X).
分析:(1)记事件A为“只有甲破译出密码”,可知:P(A)=
×(1-
)×(1-p)=
,解得P即可.
(2)由甲、乙、丙各自破译出密码的概率分别为
、
、
,利用相为对立事件的概率计算公式可得三个人不能够破译出密码的概率.X的可能取值为0、1,、2、3;P(X=0)表示三个人都没有能够破译出密码的概率,故P(X=0)=(1-
)×(1-
)×(1-
)=
;依此类推可得P(X=1),P(X=2),P(X=3)及其分布列和数学期望.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
(2)由甲、乙、丙各自破译出密码的概率分别为
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:(1)记事件A为“只有甲破译出密码”,
则P(A)=
×(1-
)×(1-p)=
,可解得p=
.
(2)X的可能取值为0、1,、2、3;
P(X=0)=(1-
)×(1-
)×(1-
)=
;P(X=1)=
×(1-
)×(1-
)+(1-
)×
×(1-
)+(1-
)×(1-
)×
=
;P(X=2)=
×
×(1-
)+
×(1-
)×
+(1-
)×
×
=
;
P(X=3)=
×
×
=
.
E(X)=0×
+1×
+2×
+3×
=
.
则P(A)=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
(2)X的可能取值为0、1,、2、3;
P(X=0)=(1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 11 |
| 24 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
P(X=3)=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 24 |
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 4 |
| 11 |
| 24 |
| 1 |
| 4 |
| 1 |
| 24 |
| 13 |
| 12 |
点评:本题考查了随机变量的概率计算方法和分布列及其数学期望、相互独立事件的概率计算公式,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
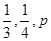 ,
,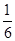 .
.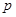 的值,
的值,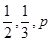 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为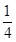 .
.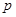 的值;
的值;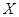 ,求
,求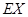 .
.