题目内容
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为
,
,p,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为
.
(1)求p的值,
(2)设在甲、乙、丙三人中破译出密码的总人数为X,求X的分布列和数学期望E(X).
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 6 |
(1)求p的值,
(2)设在甲、乙、丙三人中破译出密码的总人数为X,求X的分布列和数学期望E(X).
分析:(1)由三人中只有甲破译出密码的概率为
,列出方程
×
×(1-p)=
=
即可求得;
(2)X的可能取值为0,1,2,3,求出P(X=0),P(X=1),P(X=2),P(X=3)的值,由此能求出X的分布列和期望.
| 1 |
| 4 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1-p |
| 4 |
| 1 |
| 6 |
(2)X的可能取值为0,1,2,3,求出P(X=0),P(X=1),P(X=2),P(X=3)的值,由此能求出X的分布列和期望.
解答:解:记“甲、乙、丙三人各自破译出密码”分别为时间A,B,C
由题意得,P(A)=
,P(B)=
,P(C)=p,且A,B,C相互独立,
(1)设“三人中只有甲破译出密码”为时间D,则有
P(D)=P(A•
•
)=
×
×(1-p)=
,
所以
=
,解得,p=
.
(2)X的所有可能取值为0,1,2,3,
所以P(X=0)=
,
P(X=1)=P(A•
•
)+P(
•B•
)+P(
•
•C)=
+
×
×
+
×
×
=
,
P(X=2)=P(A•B•
)+P(A•
•C)+P(
•B•C)=
×
×
+
×
×
+
×
×
=
,
P(X=3)=P(A•B•C)=
×
×
=
.
X的分布列为:
所以E(X)=0×
+1×
+2×
+3×
=
.
由题意得,P(A)=
| 1 |
| 3 |
| 1 |
| 4 |
(1)设“三人中只有甲破译出密码”为时间D,则有
P(D)=P(A•
. |
| B |
. |
| C |
| 1 |
| 3 |
| 3 |
| 4 |
| 1-p |
| 4 |
所以
| 1-p |
| 4 |
| 1 |
| 6 |
| 1 |
| 3 |
(2)X的所有可能取值为0,1,2,3,
所以P(X=0)=
| 1 |
| 3 |
P(X=1)=P(A•
. |
| B |
. |
| C |
. |
| A |
. |
| C |
. |
| A |
. |
| B |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
| 4 |
| 9 |
P(X=2)=P(A•B•
. |
| C |
. |
| B |
. |
| A |
| 1 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 7 |
| 36 |
P(X=3)=P(A•B•C)=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 36 |
X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 3 |
| 4 |
| 9 |
| 7 |
| 36 |
| 1 |
| 36 |
| 11 |
| 12 |
点评:本题考查离散型随机变量的分布列和期望,解(1)题时要注意方程思想的运用,解(2)题时要认真审题,避免漏解.属于中档题.

练习册系列答案
相关题目
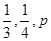 ,
,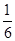 .
.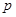 的值,
的值,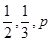 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为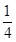 .
.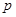 的值;
的值;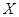 ,求
,求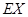 .
.