题目内容
9.设不等式组$\left\{\begin{array}{l}x≥1\\ x-2y+3≥0\\ y≥x\end{array}\right.$所表示的平面区域是Ω1,平面区域Ω2与Ω1关于直线3x-4y-9=0对称,对于Ω1中的任意一点A与Ω2中的任意一点B,|AB|的最小值等于( )| A. | 2 | B. | 4 | C. | $\frac{12}{5}$ | D. | $\frac{28}{5}$ |
分析 由题意作出可行域,数形结合得到的平面区域是Ω1内到直线3x-4y-9=0距离最小的点,由点到直线的距离公式求得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x≥1\\ x-2y+3≥0\\ y≥x\end{array}\right.$作出可行域如图,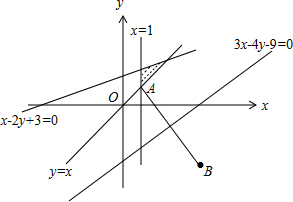
由图可知,可行域Ω1内的点A(1,1)到直线3x-4y-9=0的距离最小,
则Ω2中的点B与Ω1内的点A的距离的最小值为A到直线3x-4y-9=0的距离的2倍.
|AB|的最小值等于$2×\frac{|3×1-4×1-9|}{\sqrt{{3}^{2}+(-4)^{2}}}=4$.
故选:B.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.设a∈R,则“a=-$\frac{3}{2}$”是“直线l1:ax+2y-1=0与直线l2:x+a(a+1)y+4=0垂直”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
4.如图所示的程序框图的运行结果为S=35,那么判断框中应填入的关于k的条件是( )


| A. | k>6 | B. | k≥6 | C. | k≥7 | D. | k>7 |
1.已知函数f(x)=log2x,若在[1,8]上任取一个实数x0,则不等式1≤f(x0)≤2成立的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{7}$ | D. | $\frac{1}{2}$ |
 如图,有一景区的平面图是一半圆形,其中AB长为2km,C、D两点在半圆弧上,满足BC=CD,设∠COB=θ.
如图,有一景区的平面图是一半圆形,其中AB长为2km,C、D两点在半圆弧上,满足BC=CD,设∠COB=θ.