题目内容

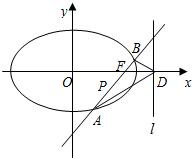精英家教网如图，椭圆Q：
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点为F（c，0），过点F的一动直线m绕点F转动，
并且交椭圆于A，B两点，P为线段AB的中点．
（1）求点P的轨迹H的方程；
（2）若在Q的方程中，令a2=1+cosθ+sinθ，b2=sinθ(0＜θ≤
π
2
)．
设轨迹H的最高点和最低点分别为M和N．当θ为何值时，△MNF为一个正三角形？
分析：（1）设出椭圆的方程，A，B的坐标和P的坐标，把A，B坐标代入椭圆的方程联立，当AB不垂直x轴时方程组相减整理求得的x和y的关系式，再看当AB垂直于x轴时，点P也满足方程，综合可得答案．
（2）把（1）中的轨迹方程整理成椭圆的标准方程，求得M，N，F的坐标，使△MNF为一个正三角形时，则tan
π
6
=
bc
2a
c
2
=
b
a
，求得a和b的关系，进而根据题设条件中的a和b的表达式，联立求得θ．
解答：解：（1）设椭圆Q：
x2
a2
+
y2
b2
=1（a＞b＞0）
上的点A（x1，y1）、B（x2，y2），又设P点坐标为P（x，y），
则
b2
x
2
1
+a2
y
2
1
=a2b2(1)
b2
x
2
2
+a2
y
2
2
=a2b2(2)

1°当AB不垂直x轴时，x1¹x2，
由（1）-（2）得
b2（x1-x2）2x+a2（y1-y2）2y=0
∴
y1-y2
x1-x2
=-
b2x
a2y
=
y
x-c

∴b2x2+a2y2-b2cx=0（3）
2°当AB垂直于x轴时，点P即为点F，满足方程（3）
故所求点P的轨迹方程为：b2x2+a2y2-b2cx=0
（2）因为轨迹H的方程可化为：
(x-
c
2
)2
a2
+
y2
b2
=(
c
2a
)2
∴M（
c
2
，
bc
2a
），N（
c
2
，-
bc
2a
），F（c，0），
使△MNF为一个正三角形时，
则tan
π
6
=
bc
2a
c
2
=
b
a
，即a2=3b2．
由于a2=1+cosθ+sinθ，b2=sinθ(0＜θ≤
π
2
)，
则1+cosq+sinq=3sinθ，
得θ=arctan
4
3
点评：本题主要考查了直线与圆锥曲线的综合问题．考查运用解析几何的方法分析问题和解决问题的能力．
练习册系列答案
相关题目
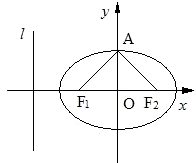精英家教网如图，椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点F1，F2和短轴的一个端点A构成等边三角形，点（
3
，
3
2
）在椭圆C上，直线l为椭圆C的左准线．
（Ⅰ）求椭圆C的方程；
（Ⅱ）点P是椭圆C上的动点，PQ⊥l，垂足为Q．是否存在点P，使得△F1PQ为等腰三角形？若存在，求出点P的坐标；若不存在，说明理由．
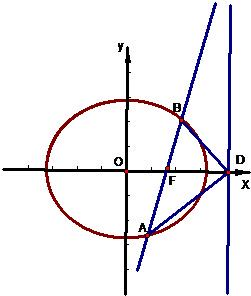精英家教网如图，椭圆Q：
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点F（c，0），过点F的一动直线m绕点F转动，并且交椭圆于A、B两点，P是线段AB的中点．
（1）求点P的轨迹H的方程．
（2）在Q的方程中，令a2=1+cosq+sinq，b2=sinq（0＜q≤
π
2
），确定q的值，使原点距椭圆的右准线l最远，此时，设l与x轴交点为D，当直线m绕点F转动到什么位置时，三角形ABD的面积最大？
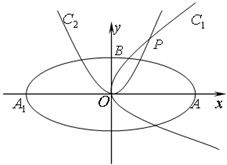精英家教网如图，椭圆C：
x2
a2
+
y2
2
=1焦点在x轴上，左、右顶点分别为A1、A，上顶点为B，抛物线C1、C2分别以A、B为焦点，其顶点均为坐标原点O．C1与C2相交于直线y=
2
x上一点P．
（Ⅰ）求椭圆C及抛物线C1、C2的方程；
（Ⅱ）若动直线l与直线OP垂直，且与椭圆C交于不同两点M、N，已知点Q(-
2
，0），求
QM
.
QN
的最小值．
（2012•山东）如图，椭圆M：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
3
2
，直线x=±a和y=±b所围成的矩形ABCD的面积为8．
（Ⅰ）求椭圆M的标准方程；
（Ⅱ）设直线l：y=x+m（m∈R）与椭圆M有两个不同的交点P，Q，l与矩形ABCD有两个不同的交点S，T．求
|PQ|
|ST|
的最大值及取得最大值时m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网