题目内容
某学校举办一场以“为希望工程献爱心”为主题的图书义卖活动,同学甲随机地从10本书中买两本,假设每本书被甲同学买走的概率相同,已知这10本书中有3本单价定为10元,4本单价定为15元,3本单价定为20元,记甲同学买这两本书所付金额为ξ(元).求:
(1)随机变量ξ的分布列;
(2)随机变量ξ的期望Eξ和方差Dξ.
解:(1)由题意可得:ξ可能取的值为:20,25,30,35,40,
所以P(ξ=2)=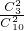 =
= ;P(ξ=25)=
;P(ξ=25)= =
= ;P(ξ=30)=
;P(ξ=30)=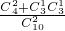 =
= =
= ;P(ξ=35)=
;P(ξ=35)= =
= ;P(ξ=40)=
;P(ξ=40)=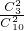 =
= ,
,
所以随机变量ξ的分布列为:
(2)由(1)可得:
随机变量ξ的期望Eξ=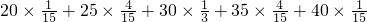 =30,
=30,
方差Dξ= +
+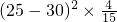 +
+ +
+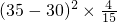 +
+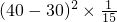 =
=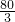 .
.
分析:(1)由题意可得:ξ可能取的值为:20,25,30,35,40,再分别求出其概率进而得到随机变量ξ的分布列.
(2)结合(1)的结论与期望与方差的计算公式即可得到答案.
点评:本题主要考查等可能事件的概率公式,以及离散型随机变量的分布列、期望与方差,此题属于基础题.
所以P(ξ=2)=
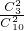 =
= ;P(ξ=25)=
;P(ξ=25)= =
= ;P(ξ=30)=
;P(ξ=30)=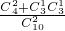 =
= =
= ;P(ξ=35)=
;P(ξ=35)= =
= ;P(ξ=40)=
;P(ξ=40)=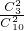 =
= ,
,所以随机变量ξ的分布列为:
| ξ | 20 | 25 | 30 | 35 | 40 |
| P |  |  |  |  |  |
随机变量ξ的期望Eξ=
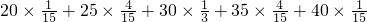 =30,
=30,方差Dξ=
 +
+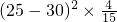 +
+ +
+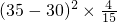 +
+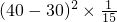 =
=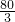 .
.分析:(1)由题意可得:ξ可能取的值为:20,25,30,35,40,再分别求出其概率进而得到随机变量ξ的分布列.
(2)结合(1)的结论与期望与方差的计算公式即可得到答案.
点评:本题主要考查等可能事件的概率公式,以及离散型随机变量的分布列、期望与方差,此题属于基础题.

练习册系列答案
相关题目