题目内容
设实数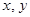
满足
向量
，
．若
，则实数
的最大值为 ．
；
解析试题分析：因为
，所以
,故根据线性规划的知识画出可行域如图,则目标函数在点（1，8）处取得最大值6.
考点：向量平行 线性规划
练习册系列答案
相关题目
题目内容
设实数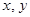满足 向量，．若，则实数的最大值为 ．
；
解析试题分析：因为，所以,故根据线性规划的知识画出可行域如图,则目标函数在点（1，8）处取得最大值6.
考点：向量平行 线性规划
， 若z的最大值为12，则实数k= ．
及其内部,若目标函数
当且仅当在点
处取得最大值,则
的取值范围是______.
满足
，过点P的直线l与圆
相交于A、B两点，则AB的最小值为 .
所表示的平面区域为
，记
. 则
＝ ，经推理可得到
= ．
，若目标函数
（
）的最大值为8，则
的最小值为 .
中，记不等式组
所表示的平面区域为
.在映射
的作用下，区域
对应的象为点
. 
的作用下，点
的原象是 ；
则目标函数z＝x＋y的最大值为________．
令点集T＝{(x0，y0)∈D|x0，y0∈Z，(x0，y0)是z＝x＋y在D上取得最大值或最小值的点}，则T中的点共确定________条不同的直线．