题目内容
在△ABC中，AB=5，AC=7，∠A=60°，G为重心，过G的平面α与BC平行，AB∩α=M，AC∩α=N，则MN=分析：由已知AB=5，AC=7，∠A=60利用余弦定理可求BC，根据线面平行的性质定理可得，MN∥BC，且G是△ABC的重心可得MN=
BC
从而可求MN
| 2 |
| 3 |
从而可求MN
解答：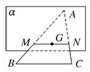
解：如图，在△ABC中，由余弦定理知BC=
，
∵BC∥α，AB∩α=M，AC∩α=N，
根据线面平行的性质定理可得，MN∥BC，
又G是△ABC的重心，
∴MN=
BC=
．
故答案为：
解：如图，在△ABC中，由余弦定理知BC=| 39 |
∵BC∥α，AB∩α=M，AC∩α=N，
根据线面平行的性质定理可得，MN∥BC，
又G是△ABC的重心，
∴MN=
| 2 |
| 3 |
2
| ||
| 3 |
故答案为：
2
| ||
| 3 |
点评：本题主要考查了余弦定理解决三角形中两边和夹角求第三边，直线与平面平行的性质定理的运用，三角形的重心的性质等知识的运用．
练习册系列答案
一本好题口算题卡系列答案
相关题目