题目内容
设一直角三角形的两条直角边长均是区间
上的任意实数，则斜边长小于
的概率为 ．
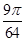
解析试题分析：不妨设直角三角形的两条直角边长为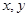
,则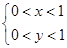
表示的区域如图所示为一个边长为1的正方形,即面积
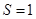,根据勾股定理可得斜边长
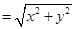,则根据题意可得
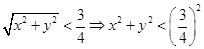,即点
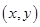在以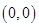
为圆心,半径为的圆内,则即在园内又在正方形区域内的面积为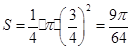
,则根据几何概型的概率计算公式可得
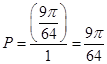,故填.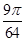
考点：几何概型 勾股定理
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
之间的均匀随机数
,则事件“
”发生的概率为_______．
，在操作考试中“合格”的概率依次为
，所有考试是否合格，相互之间没有影响．则甲、乙进行理论与操作两项考试后，恰有1人获得“合格证书”的概率 ．