题目内容
已知圆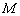 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ,点
,点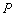 在直线
在直线 上,过
上,过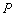 点作圆
点作圆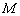 的切线
的切线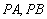 ,切点为
,切点为 .
.
(1)若 ,试求点
,试求点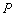 的坐标;
的坐标;
(2)若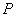 点的坐标为
点的坐标为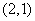 ,过
,过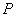 作直线与圆
作直线与圆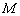 交于
交于 两点,当
两点,当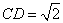 时,求直线
时,求直线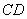 的方程;
的方程;
(3)求证:经过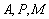 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
【答案】
解:(1)设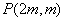 ,由题可知
,由题可知 ,所以
,所以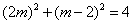 ,解之得:
,解之得: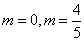
故所求点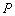 的坐标为
的坐标为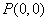 或
或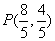 . …………………………………………4分
. …………………………………………4分
(2)设直线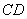 的方程为:
的方程为: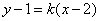 ,易知
,易知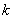 存在,由题知圆心
存在,由题知圆心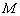 到直线
到直线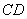 的距离为
的距离为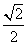 ,所以
,所以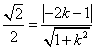 , …………………………………………6分
, …………………………………………6分
解得,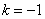 或
或 ,
,
故所求直线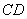 的方程为:
的方程为: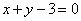 或
或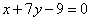 .………………………8分
.………………………8分
(3)设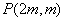 ,
,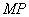 的中点
的中点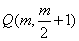 ,因为
,因为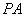 是圆
是圆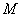 的切线
的切线
所以经过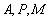 三点的圆是以
三点的圆是以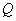 为圆心,以
为圆心,以 为半径的圆,
为半径的圆,
故其方程为: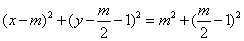 ……………………………10分
……………………………10分
化简得: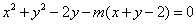 ,此式是关于
,此式是关于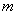 的恒等式,
的恒等式,
故 解得
解得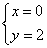 或
或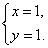
所以经过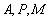 三点的圆必过定点
三点的圆必过定点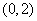 或
或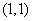 .…………………………………14分
.…………………………………14分

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
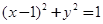 ,直线l的方程为
,直线l的方程为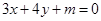 ,若圆与直线相切,则实数m=
.
,若圆与直线相切,则实数m=
.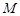 的方程为
的方程为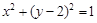 ,直线
,直线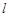 的方程为
的方程为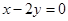 ,点
,点 在直线
在直线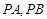 ,切点为
,切点为 .
.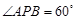 ,试求点
,试求点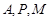 三点的圆必过定点,并求出所有定点的坐标;
三点的圆必过定点,并求出所有定点的坐标;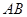 长的最小值.
长的最小值. 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ,点
,点 在直线
在直线 ,切点为
,切点为 .
. ,试求点
,试求点 点的坐标为
点的坐标为 ,过
,过 两点,当
两点,当 时,求直线
时,求直线 的方程;ks.5u
的方程;ks.5u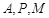 三点的圆是否经过异于点M的定点,若经过,请求出此定点的坐标;若不经过,请说明理由。
三点的圆是否经过异于点M的定点,若经过,请求出此定点的坐标;若不经过,请说明理由。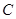 的方程为:
的方程为: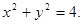 直线
直线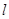 过点
过点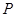 (1,2),且与圆
(1,2),且与圆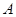 、
、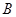 两点,若
两点,若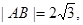 求直线
求直线 .直线方程为L:
.直线方程为L: ,则直线L与圆的位置关系是 ( )
,则直线L与圆的位置关系是 ( )