题目内容
已知圆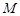 的方程为
的方程为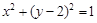 ,直线
,直线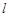 的方程为
的方程为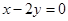 ,点
,点 在直线
在直线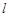 上,过
上,过 点作圆
点作圆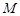 的切线
的切线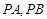 ,切点为
,切点为 .
.
(1)若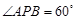 ,试求点
,试求点 的坐标;
的坐标;
(2)求证:经过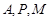 三点的圆必过定点,并求出所有定点的坐标;
三点的圆必过定点,并求出所有定点的坐标;
(3)求弦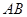 长的最小值.
长的最小值.
【答案】
(1)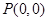 或
或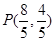 ;(2)见解析;(3)
;(2)见解析;(3)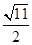 .
.
【解析】(1)根据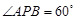 ,求得
,求得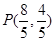 ;(2)求出圆的方程
;(2)求出圆的方程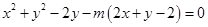 ,此式是关于
,此式是关于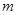 的恒等式,列条件;(3)表示出弦长,求最值。
的恒等式,列条件;(3)表示出弦长,求最值。
解:(1)设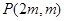 ,由题可知
,由题可知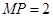 ,所以
,所以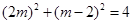 ,解之得:
,解之得: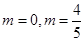 故所求点
故所求点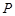 的坐标为
的坐标为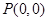 或
或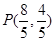 .
........4分
.
........4分
(2)设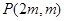 ,
,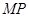 的中点
的中点 ,因为
,因为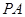 是圆
是圆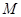 的切线
的切线
所以经过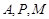 三点的圆是以
三点的圆是以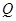 为圆心,以
为圆心,以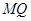 为半径的圆,
为半径的圆,
故其方程为: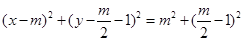 ........6分
........6分
化简得: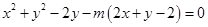 ,此式是关于
,此式是关于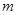 的恒等式,
的恒等式,
故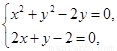 解得
解得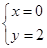 或
或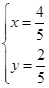
所以经过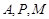 三点的圆必过定点
三点的圆必过定点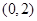 或
或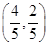 .
........10分
.
........10分
(3)设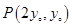 ,且
,且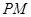 与
与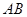 交于点
交于点 ,则
,则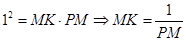
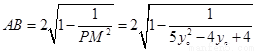 当
当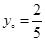 时,
时,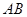 最小值为
最小值为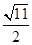 ...16分
...16分
(几何方法酌情给分)

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
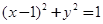 ,直线l的方程为
,直线l的方程为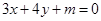 ,若圆与直线相切,则实数m=
.
,若圆与直线相切,则实数m=
. 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ,点
,点 在直线
在直线 ,切点为
,切点为 .
. ,试求点
,试求点 点的坐标为
点的坐标为 ,过
,过 两点,当
两点,当 时,求直线
时,求直线 的方程;ks.5u
的方程;ks.5u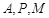 三点的圆是否经过异于点M的定点,若经过,请求出此定点的坐标;若不经过,请说明理由。
三点的圆是否经过异于点M的定点,若经过,请求出此定点的坐标;若不经过,请说明理由。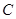 的方程为:
的方程为: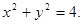 直线
直线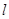 过点
过点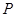 (1,2),且与圆
(1,2),且与圆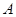 、
、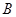 两点,若
两点,若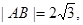 求直线
求直线 .直线方程为L:
.直线方程为L: ,则直线L与圆的位置关系是 ( )
,则直线L与圆的位置关系是 ( )