题目内容
对于R上可导的任意函数f(x),且 若满足(x-1)
若满足(x-1) >0,则必有( )
>0,则必有( )
| A.f(0)+f(2)<2f(1) | B.f(0)+f(2)³2f(1) |
| C.f(0)+f(2)>2f(1) | D.f(0)+f(2)³2f(1) |
C
解析试题分析:因为,(x-1) >0,所以在区间(1,+
>0,所以在区间(1,+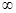 ),
), >0,函数f(x)是增函数;在区间(-
>0,函数f(x)是增函数;在区间(-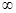 ,1),
,1), <0,函数f(x)是减函数,又
<0,函数f(x)是减函数,又 ,所以,x=1是极小值点,f(0)>f(1),f(2)>f(1),因此f(0)+f(2)>2f(1),故选C。
,所以,x=1是极小值点,f(0)>f(1),f(2)>f(1),因此f(0)+f(2)>2f(1),故选C。
考点:本题主要考查应用导数研究函数的单调性,不等式性质。
点评:小综合题,在某区间,导函数值非负,则函数为增函数;导函数值非正,则函数为减函数。

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
已知点 在曲线
在曲线 上,
上, 为曲线在点
为曲线在点 处的切线的倾斜角,则
处的切线的倾斜角,则 取值范围是
取值范围是
A.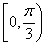 | B. | C.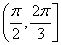 | D. |
在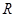 上可导的函数
上可导的函数 的图形如图所示,则关于
的图形如图所示,则关于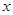 的不等式
的不等式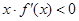 的解集为( )
的解集为( )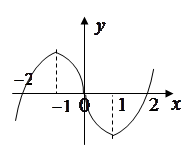
A.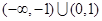 | B.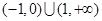 |
C.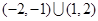 | D.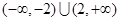 |
已知函数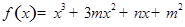 在
在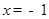 时有极值为0,则m+n=( )
时有极值为0,则m+n=( )
| A.11 | B.4或11 | C.4 | D.8 |
定义在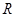 上的可导函数
上的可导函数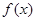 ,当
,当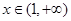 时,
时,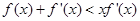 恒成立,
恒成立,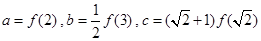 ,则
,则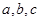 的大小关系为 ( )
的大小关系为 ( )
A.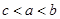 | B.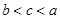 | C.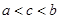 | D. |
已知定义域为R的函数 满足:
满足: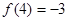 ,且对任意
,且对任意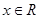 总有
总有 <3,则不等式
<3,则不等式 的解集为( )
的解集为( )
A.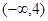 | B. | C. | D. |
曲线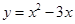 上点P 处切线平行与
上点P 处切线平行与 轴,则P点坐标为( )
轴,则P点坐标为( )
A.(- , , 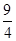 ) ) | B.( ,- ,-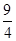 ) ) | C.(- ,- ,-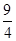 ) ) | D.( , , 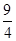 ) ) |
设等差数列{an}的前n项和为Sn,已知(a5-1)3+2 011·(a5-1)=1,(a2 007-1)3+2 011(a2 007-1)=-1,则下列结论正确的是( )
| A.S2 011=2 011,a2 007<a5 | B.S2 011=2 011,a2 007>a5 |
| C.S2 011=-2 011,a2 007≤a5 | D.S2 011=-2 011,a2 007≥a5 |