题目内容
9.下列说法及计算不正确的命题序号是④①6名学生争夺3项冠军,冠军的获得情况共有36种;
②某校开设A类选修课3门,B类选修课4门,一位同学从中共选3门,若要求两类课程中各至少一门,则不同的选法共有60种;
③对于任意实数x,有f(-x)=-f(x),g(-x)=g(x),且x>0,f′(x)<0,g′(x)<0,则x<0,f′(x)>0,g′(x)<0;
④${∫}_{a}^{b}$f(x)dx=${∫}_{a}^{c}$f(x)dx+${∫}_{c}^{b}$f(x)dx(a<c<b).
分析 ①由题意可得每项冠军获得情况都有6中可能,由分步乘法原理求得冠军的获得情况后加以判断;
②两类课程中各至少选一门,包含两种情况:A类选修课选1门,B类选修课选2门;A类选修课选2门,B类选修课选1门,写出组合数,根据分类计数原理得到结果;
③先利用函数奇偶性的定义判断出f(x),g(x)的奇偶性;利用导数与函数的单调性的关系判断出两个函数在(0,+∞)上的单调性,再据奇函数在对称区间上的单调性相同,偶函数在对称区间上的单调性相反得到f(x),g(x)在(-∞,0)的单调性,再利用导数与函数的单调性的关系判断出两个导函数的符号;
④由积分公式说明正确.
解答 解:①6名学生争夺3项冠军,每项冠军获得情况都有6中可能,由分步乘法原理可得共有63种,①错误;
②可分以下2种情况:A类选修课选1门,B类选修课选2门,有C31C42种不同的选法;A类选修课选2门,B类选修课选1门,有C32C41种不同的选法.
∴根据分类计数原理知不同的选法共有C31C42+C32C41=18+12=30种,②错误;
③∵对任意实数x,有f(-x)=-f(x),g(-x)=g(x),
∴f(x)为奇函数;g(x)为偶函数
∵x>0时,f′(x)<0,g′(x)<0,
∴f(x)在(0,+∞)上为减函数;g(x)在(0,+∞)上为减函数,
∴f(x)在(-∞,0)上为减函数;g(x)在(-∞,0)上为增函数,
∴f′(x)<0;g′(x)>0,则③错误;
④由${∫}_{a}^{b}$f(x)dx=${∫}_{a}^{c}$f(x)dx+${∫}_{c}^{b}$f(x)dx(a<c<b),可知④正确.
故答案为:④.
点评 本题考查命题的真假判断与应用,考查了简单的排列组合问题,训练了利用函数导函数的符号判断原函数的单调性,属中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 4500 | B. | 4505 | C. | 4514 | D. | 4519 |
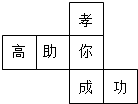 水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )
水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )| A. | 左面,后面,上面 | B. | 后面,上面,左面 | C. | 上面,左面,后面 | D. | 后面,左面,上面 |
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
| A. | 2∈P | B. | 2∉P | C. | 2⊆P | D. | 2?P |