题目内容
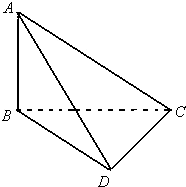
如图,已知△ABC和△DBC所在的平面互相垂直,AB=BC=BD,∠CBA=∠DBC=120°,求:(1)AD与BC所成的角;
(2)AD和平面BCD所成的角;
(3)二面角A-BD-C的大小的余弦值.

【答案】分析:(1)作AO⊥BC于点O,连DO,以点O为原点,OD,OC,OA的方向分别为x轴、y轴、z轴方向,建立坐标系,通过 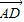 与
与  的夹角去求AD与BC所成的角.
的夹角去求AD与BC所成的角.
(2)通过求 与平面BCD的夹角去求AD和平面BCD所成的角.
与平面BCD的夹角去求AD和平面BCD所成的角.
(3)求出平面CBD的一个法向量为 以及平面ABD的一个法向量为
以及平面ABD的一个法向量为  ,求出两法向量的余弦值即可得到平面CDF与平面ABCD所成角的余弦值.
,求出两法向量的余弦值即可得到平面CDF与平面ABCD所成角的余弦值.
解答:解:(1)设AB=1,作AO⊥BC于点O,连DO,以点O为原点,OD,OC,OA的方向分别为x轴、y轴、z轴方向,建立坐标系,得下列坐标:
O(0,0,0)D( ,0,0)B(0,
,0,0)B(0, ,0)C(0,
,0)C(0, ,0)A(0,0,
,0)A(0,0, )
)
 =(
=( ,0,-
,0,-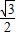 ),
),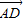 •
• =(
=( ,0,-
,0,- )•(0,1,0)=0
)•(0,1,0)=0
所以AD与BC所成角等于90°.
(2)由(1)可知 =(0,0,1)为平面BCD的一个法向量
=(0,0,1)为平面BCD的一个法向量
|cos<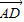 ,
, >|=|
>|=| |=|-
|=|- |=
|=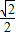
∴直线AD与平面BCD所成角的大小90°-45°=45°
(3)设平面ABD的法向量为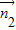 =(x,y,1)则
=(x,y,1)则
(x,y,1)•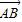 =(x,y,1)•(0,
=(x,y,1)•(0, ,-
,-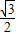 )=0
)=0
(x,y,1)•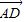 =(x,y,1)•(
=(x,y,1)•(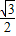 ,0,-
,0,- )=0
)=0
解得 x=1,y= ,
,
则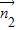 =(1,
=(1, ,1)
,1)
显然(0,0,1)为平面BCD的法向量.
设二面角A-BD-C大小为θ,则
|cosθ|=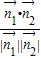 =
=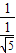 =
=
又 二面角A-BD-C为钝二面角
因此,二面角的余弦为 .
.
(第一问中含建立坐标系2分)
点评:本题考查空间角的计算,二面角求解,考查转化的思想方法,计算能力.利用空间向量的知识,则使问题论证变成了代数运算,使人们解决问题更加方便.
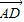 与
与  的夹角去求AD与BC所成的角.
的夹角去求AD与BC所成的角.(2)通过求
 与平面BCD的夹角去求AD和平面BCD所成的角.
与平面BCD的夹角去求AD和平面BCD所成的角.(3)求出平面CBD的一个法向量为
 以及平面ABD的一个法向量为
以及平面ABD的一个法向量为  ,求出两法向量的余弦值即可得到平面CDF与平面ABCD所成角的余弦值.
,求出两法向量的余弦值即可得到平面CDF与平面ABCD所成角的余弦值.解答:解:(1)设AB=1,作AO⊥BC于点O,连DO,以点O为原点,OD,OC,OA的方向分别为x轴、y轴、z轴方向,建立坐标系,得下列坐标:
O(0,0,0)D(
 ,0,0)B(0,
,0,0)B(0, ,0)C(0,
,0)C(0, ,0)A(0,0,
,0)A(0,0, )
) =(
=( ,0,-
,0,-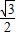 ),
),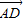 •
• =(
=( ,0,-
,0,- )•(0,1,0)=0
)•(0,1,0)=0所以AD与BC所成角等于90°.
(2)由(1)可知
 =(0,0,1)为平面BCD的一个法向量
=(0,0,1)为平面BCD的一个法向量|cos<
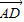 ,
, >|=|
>|=| |=|-
|=|- |=
|=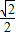
∴直线AD与平面BCD所成角的大小90°-45°=45°
(3)设平面ABD的法向量为
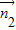 =(x,y,1)则
=(x,y,1)则(x,y,1)•
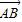 =(x,y,1)•(0,
=(x,y,1)•(0, ,-
,-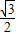 )=0
)=0(x,y,1)•
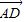 =(x,y,1)•(
=(x,y,1)•(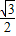 ,0,-
,0,- )=0
)=0解得 x=1,y=
 ,
,则
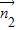 =(1,
=(1, ,1)
,1)显然(0,0,1)为平面BCD的法向量.
设二面角A-BD-C大小为θ,则
|cosθ|=
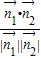 =
=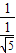 =
=
又 二面角A-BD-C为钝二面角
因此,二面角的余弦为
 .
.(第一问中含建立坐标系2分)
点评:本题考查空间角的计算,二面角求解,考查转化的思想方法,计算能力.利用空间向量的知识,则使问题论证变成了代数运算,使人们解决问题更加方便.

练习册系列答案
相关题目
 如图,已知△ABC和△BCD所在平面互相垂直,∠ABC=∠BCD=90°,AB=a,BC=b,CD=c,且a2+b2+c2=1,则三棱锥A-BCD的外接球的表面积为
如图,已知△ABC和△BCD所在平面互相垂直,∠ABC=∠BCD=90°,AB=a,BC=b,CD=c,且a2+b2+c2=1,则三棱锥A-BCD的外接球的表面积为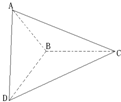 如图,已知△ABC和△DBC所在的平面互相垂直,AB=BC=BD,∠CBA=∠DBC=120°,求:
如图,已知△ABC和△DBC所在的平面互相垂直,AB=BC=BD,∠CBA=∠DBC=120°,求: 如图,已知△ABC和△BCD所在平面互相垂直,∠ABC=∠BCD=90°,AB=a,BC=b,CD=c,且a2+b2+c2=1,则三棱锥A-BCD的外接球的表面积为 .
如图,已知△ABC和△BCD所在平面互相垂直,∠ABC=∠BCD=90°,AB=a,BC=b,CD=c,且a2+b2+c2=1,则三棱锥A-BCD的外接球的表面积为 . 如图,已知△ABC和△BCD所在平面互相垂直,∠ABC=∠BCD=90°,AB=a,BC=b,CD=c,且a2+b2+c2=1,则三棱锥A-BCD的外接球的表面积为 .
如图,已知△ABC和△BCD所在平面互相垂直,∠ABC=∠BCD=90°,AB=a,BC=b,CD=c,且a2+b2+c2=1,则三棱锥A-BCD的外接球的表面积为 .