题目内容
如图，已知△ABC和△BCD所在平面互相垂直，∠ABC=∠BCD=90°，AB=a，BC=b，CD=c，且a2+b2+c2=1，则三棱锥A-BCD的外接球的表面积为 ．
【答案】分析：要求外接球，需知到其半径，因为球心到球面的点的距离相等，可以找出一点到ABCD四个点的距离相等，求解即可．
解答：解：因为球心到球面的点的距离相等，可以找出一点到ABCD四个点的距离相等，在直角三角形中斜边上的中点到各顶点距离相等，
可知AD中点O到A，B，C，D的距离相等，所以AO=
所以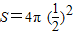
=π
点评：本题考查学生的空间想象能力，以及对三角形的性质的使用，是基础题．
解答：解：因为球心到球面的点的距离相等，可以找出一点到ABCD四个点的距离相等，在直角三角形中斜边上的中点到各顶点距离相等，
可知AD中点O到A，B，C，D的距离相等，所以AO=
所以
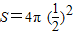=π点评：本题考查学生的空间想象能力，以及对三角形的性质的使用，是基础题．
练习册系列答案
相关题目
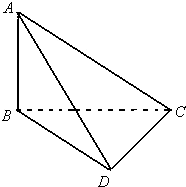如图，已知△ABC和△BCD所在平面互相垂直，∠ABC=∠BCD=90°，AB=a，BC=b，CD=c，且a2+b2+c2=1，则三棱锥A-BCD的外接球的表面积为
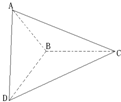如图，已知△ABC和△DBC所在的平面互相垂直，AB=BC=BD，∠CBA=∠DBC=120°，求：
如图，已知△ABC和△BCD所在平面互相垂直，∠ABC=∠BCD=90°，AB=a，BC=b，CD=c，且a2+b2+c2=1，则三棱锥A-BCD的外接球的表面积为 ．