题目内容
如图,在多面体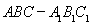 中,四边形
中,四边形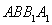 是正方形,
是正方形,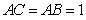 ,
,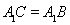 ,
,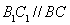 ,
,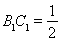
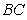 .
.
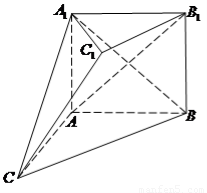
(1)求证:面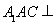 面
面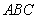 ;
;
(2)求证: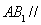 面
面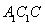 .
.
【答案】
(1)证明见解析;(2)见解析.
【解析】
试题分析:(1)要证明面面垂直,需先证线面垂直.
利用四边形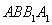 为正方形,证得
为正方形,证得 ,即
,即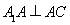 ,
,
再根据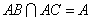 ,
,
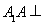 面
面
得证.
(2)注意利用“平行关系的传递性”.
通过取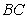 的中点
的中点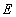 ,连结
,连结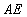 ,
,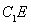 ,
,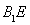
应用三角形中位线定理得出四边形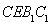 为平行四边形,即
为平行四边形,即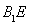
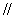
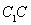
从而得到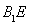
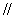 面
面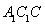 ;
;
类似地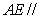 面
面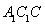 ,由面
,由面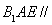 面
面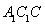
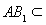 面
面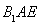 ,得出
,得出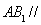 面
面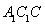 .
.
试题解析:证明:(1) 四边形
四边形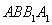 为正方形,
为正方形, 
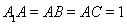 ,
, 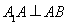

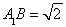 2分
2分

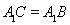

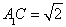



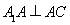 4分
4分

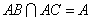 ,
,
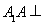 面
面
又
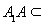 面
面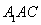 ,
, 面
面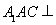 面
面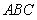 6分
6分

(2)取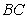 的中点
的中点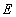 ,连结
,连结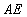 ,
,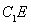 ,
,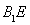

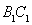
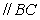 ,
,
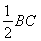 ,
,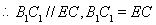
 四边形
四边形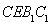 为平行四边形
为平行四边形

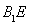
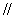
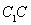

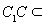 面
面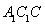 ,
, 面
面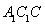

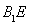
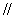 面
面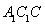 8分
8分

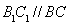 ,
,
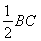 ,
,
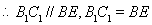
 四边形
四边形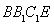 为平行四边形
为平行四边形
 ,且
,且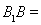
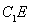
又
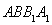 是正方形,
是正方形,
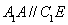 ,且
,且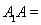
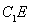

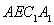 为平行四边形,
为平行四边形,
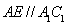 ,
,
 面
面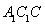 ,
,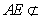 面
面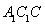

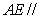 面
面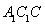 10分
10分

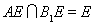 ,
, 面
面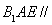 面
面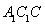

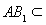 面
面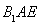 ,
,
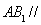 面
面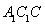 12分
12分
考点:空间的平行关系,三角形中位线定理,平行四边形的性质.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:①3;②4; ③5;④6;⑤7.以上结论正确的为
多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:①3;②4; ③5;④6;⑤7.以上结论正确的为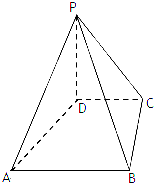 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=2DC,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=2DC,AB∥DC,∠BCD=90°.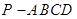 中,
中,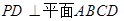 ,
,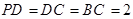 ,
, ,
,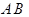 ∥
∥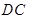 ,
,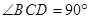 .
.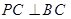 ;
;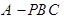 的体积.
的体积.
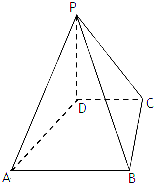 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=2DC,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=2DC,AB∥DC,∠BCD=90°.