题目内容
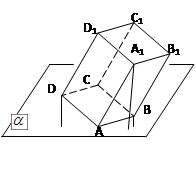
 多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:①3;②4; ③5;④6;⑤7.以上结论正确的为
多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:①3;②4; ③5;④6;⑤7.以上结论正确的为分析:根据题意,一一验证正方体的各个顶点到平面α的距离即可进行判断,为了求出各个顶点到平面α的距离,注意应用中点的纽带作用.
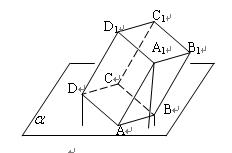
解答: 解:如图,B、D、A1到平面α的距离分别为1、2、4,
解:如图,B、D、A1到平面α的距离分别为1、2、4,
则D、A1的中点到平面α的距离为3,即
A、D1的中点到平面α的距离为3
所以D1到平面α的距离为6;同样地,
B、A1的中点到平面α的距离为
,
所以B1到平面α的距离为5;
则D、B的中点到平面α的距离为
,
所以C到平面α的距离为3;
C、A1的中点到平面α的距离为
,
所以C1到平面α的距离为7;
而P为C、C1、B1、D1中的一点,
所以选①③④⑤.
 解:如图,B、D、A1到平面α的距离分别为1、2、4,
解:如图,B、D、A1到平面α的距离分别为1、2、4,则D、A1的中点到平面α的距离为3,即
A、D1的中点到平面α的距离为3
所以D1到平面α的距离为6;同样地,
B、A1的中点到平面α的距离为
| 5 |
| 2 |
所以B1到平面α的距离为5;
则D、B的中点到平面α的距离为
| 3 |
| 2 |
所以C到平面α的距离为3;
C、A1的中点到平面α的距离为
| 7 |
| 2 |
所以C1到平面α的距离为7;
而P为C、C1、B1、D1中的一点,
所以选①③④⑤.
点评:本题主要考查了点、线、面间的距离计算,考查空间想象能力、运算能力和推理论证能力,属于创新题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
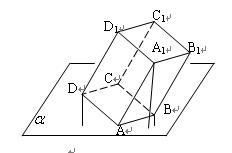
 内,其余顶点在
内,其余顶点在