题目内容
函数 是定义域为R的奇函数,且
是定义域为R的奇函数,且 时,
时, ,则函数
,则函数 的零点个数是( )
的零点个数是( )
| A.1 | B.2 | C.3 | D.4 |
C
解析试题分析:由题意知 ,当
,当 时,令
时,令 ,即
,即 ,
,
令 ,
, ,
, 当
当 时,
时,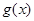 与
与 有1个交点,即
有1个交点,即 时
时 有1个零点,又
有1个零点,又 是定义域为R的奇函数,所以函数
是定义域为R的奇函数,所以函数 有3个零点.
有3个零点.
考点:奇函数的性质、零点问题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
给定函数:① ;②
;② ;③
;③ ;④
;④ ,其中奇函数是( )
,其中奇函数是( )
| A.① | B.② | C.③ | D.④ |
函数 的零点的个数为( )
的零点的个数为( )
A. | B.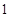 | C. | D.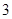 |
定义在 上的奇函数
上的奇函数 ,满足
,满足 ,
, ,则函数
,则函数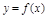 在区间
在区间 内零点个数的情况为( )
内零点个数的情况为( )
A. 个 个 | B. 个 个 | C. 个 个 | D.至少 个 个 |
已知函数 的反函数
的反函数 满足
满足 ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
设 是定义在实数集
是定义在实数集 上的函数,满足条件
上的函数,满足条件 是偶函数,且当
是偶函数,且当 时,
时, ,则
,则 ,
, ,
, 的大小关系是( )
的大小关系是( )
A. |
B. |
C.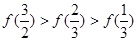 |
D. |
下列函数中,最小值为4的函数是( )
A. | B. |
C. | D. |
已知函数 为奇函数,且当
为奇函数,且当 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
 的反函数
的反函数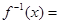 ________________.
________________.