题目内容
某射手向一个气球射击,假定各次射击是相互独立的,且每次射击击破气球的概率均为 .
.(I)若该射手共射击三次,求第三次射击才将球击破的概率;
(II)给出两种积分方案:
方案甲:提供三次射击机会和一张700点的积分卡,若未击中的次数为ξ,则扣除积分128ξ点.
方案乙:提供四次射击机会和一张1000点的积分卡,若未击中的次数为ξ,则扣除积分256ξ点.
在执行上述两种方案时规定:若将球击破,则射击停止;若未击破,则继续射击直至用完规定的射击次数.
问:该射手应选择哪种方案才能使积分卡剩余点数最多,并说明理由.
【答案】分析:(I)设Ai表示第i次将球击破,则P=P(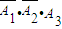 ),由此能求出第三次射击才将球击破的概率.
),由此能求出第三次射击才将球击破的概率.
(II)对于方案甲,积分卡剩余点数η甲=700-128ξ,ξ=0,1,2,3;对于方案乙,积分卡剩余点数η乙=1000-256ξ,ξ=0,1,2,3,4.分别求出Eη甲和Eη乙,能得到结果.
解答:解:(I)设Ai表示第i次将球击破,
则P=P(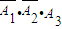 )=
)=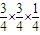 =
=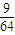 .(5分)
.(5分)
(II)对于方案甲,积分卡剩余点数η甲=700-128ξ,ξ=0,1,2,3,
由已知可得P(ξ=0)= ,
,
P(ξ=1)=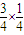 =
=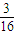 ,
,
P(ξ=2)=( )2×
)2× =
=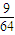 ,
,
P(ξ=3)=( )3=
)3=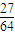 .
.
故Eξ=0× +1×
+1×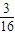 +2×
+2×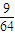 +3×
+3×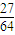 =
=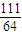 .
.
故Eη甲=E(700-128ξ)=700-128Eξ=478.(8分)
对于方案乙,积分卡剩余点数η乙=1000-256ξ,ξ=0,1,2,3,4,
由已知可得P(ξ=0)= ,
,
P(ξ=1)=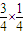 =
=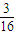 ,
,
P(ξ=2)=( )2×
)2× =
=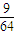 ,
,
P(ξ=3)=( )3×
)3× =
=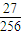 ,
,
P(ξ=4)=( )4=
)4=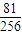
∴Eξ=0× +1×
+1×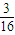 +2×
+2×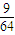 +3
+3 +4×
+4×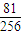 =
= .
.
故Eη乙=E(1000-256ξ)=1000-Eξ=475.(11分)
故Eη甲>Eη乙,
所以选择方案甲积分卡剩余点数最多.(12分)
点评:本题考查离散型随机变量的数学期望的应用,解题时要认真审题,仔细解答,注意排列组合知识的合理运用.
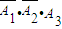 ),由此能求出第三次射击才将球击破的概率.
),由此能求出第三次射击才将球击破的概率.(II)对于方案甲,积分卡剩余点数η甲=700-128ξ,ξ=0,1,2,3;对于方案乙,积分卡剩余点数η乙=1000-256ξ,ξ=0,1,2,3,4.分别求出Eη甲和Eη乙,能得到结果.
解答:解:(I)设Ai表示第i次将球击破,
则P=P(
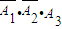 )=
)=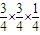 =
=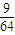 .(5分)
.(5分)(II)对于方案甲,积分卡剩余点数η甲=700-128ξ,ξ=0,1,2,3,
由已知可得P(ξ=0)=
 ,
,P(ξ=1)=
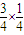 =
=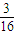 ,
,P(ξ=2)=(
 )2×
)2× =
=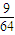 ,
,P(ξ=3)=(
 )3=
)3=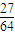 .
.故Eξ=0×
 +1×
+1×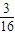 +2×
+2×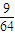 +3×
+3×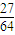 =
=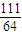 .
.故Eη甲=E(700-128ξ)=700-128Eξ=478.(8分)
对于方案乙,积分卡剩余点数η乙=1000-256ξ,ξ=0,1,2,3,4,
由已知可得P(ξ=0)=
 ,
,P(ξ=1)=
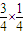 =
=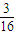 ,
,P(ξ=2)=(
 )2×
)2× =
=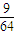 ,
,P(ξ=3)=(
 )3×
)3× =
=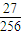 ,
,P(ξ=4)=(
 )4=
)4=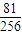
∴Eξ=0×
 +1×
+1×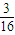 +2×
+2×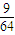 +3
+3 +4×
+4×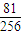 =
= .
.故Eη乙=E(1000-256ξ)=1000-Eξ=475.(11分)
故Eη甲>Eη乙,
所以选择方案甲积分卡剩余点数最多.(12分)
点评:本题考查离散型随机变量的数学期望的应用,解题时要认真审题,仔细解答,注意排列组合知识的合理运用.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目