题目内容
下面几个命题中,假命题是( )
A.“若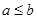 ,则 ,则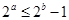 ”的否命题; ”的否命题; |
B.“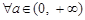 ,函数 ,函数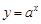 在定义域内单调递增”的否定; 在定义域内单调递增”的否定; |
C.“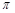 是函数 是函数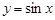 的一个周期”或“ 的一个周期”或“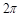 是函数 是函数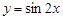 的一个周期”; 的一个周期”; |
D.“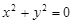 ”是“ ”是“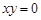 ”的必要条件. ”的必要条件. |
D
解析试题分析:选项A的命题的否命题为“若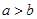 ,则
,则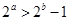 ”,该命题为真命题.选项B的命题的否定为“
”,该命题为真命题.选项B的命题的否定为“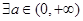 ,函数
,函数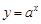 在定义域内不单调递增” ,
在定义域内不单调递增” ,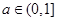 该命题为真命题.选项C是用“或”连接的复合命题,所以要两个命题都是假命题复合命题才是假命题.由“
该命题为真命题.选项C是用“或”连接的复合命题,所以要两个命题都是假命题复合命题才是假命题.由“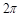 是函数
是函数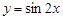 的一个周期”是真命题,所以C选项的命题是真命题.由于“
的一个周期”是真命题,所以C选项的命题是真命题.由于“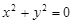 ”是“
”是“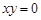 ”的充分不必要条件.所以D选项的命题不正确.
”的充分不必要条件.所以D选项的命题不正确.
考点:1.命题的知识.2.命题的否定.3.否命题.4.函数知识.5.充要条件.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
已知命题 :复数
:复数 在复平面内所对应的点位于第四象限;命题
在复平面内所对应的点位于第四象限;命题 :
: ,
, ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )
A. | B. | C. | D. |
若命题“ 使得
使得 ”为假命题,则实数
”为假命题,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
命题“对任意的 ”的否定是( )
”的否定是( )
A.存在 |
B.存在 |
C.不存在 |
D.对任意的 |
[2012·浙江高考]设a∈R,则“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分又不必要条件 |
(2011•山东)已知a,b,c∈R,命题“若a+b+c=3,则a2+b2+c2≥3”的否命题是( )
| A.若a+b+c≠3,则a2+b2+c2<3 | B.若a+b+c=3,则a2+b2+c2<3 |
| C.若a+b+c≠3,则a2+b2+c2≥3 | D.若a2+b2+c2≥3,则a+b+c=3 |
如果命题“p且q”是假命题,“非p”是真命题,那么( )
| A.命题p一定是真命题 |
| B.命题q一定是真命题 |
| C.命题q可以是真命题也可以是假命题 |
| D.命题q一定是假命题 |
设集合A={x∈R|x-2>0},B={x∈R|x<0},C={x∈R|x(x-2)>0},则“x∈A∪B”是“x∈C”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |