题目内容
12.已知集合A={x||x-1|<2},$B=\{x|\frac{{x({x-4})}}{{({x-1})({x-2})}}≤0\}$,U=R,求A∩B,A∪B,A∩(CUB).分析 找出两集合中解集的公共部分,求出两集合的交集;找出既属于A又属于B的部分,求出两集合的并集;找出全集中不属于B的部分,求出B的补集,找出A与B补集的公共部分,即可确定出所求的集合.
解答 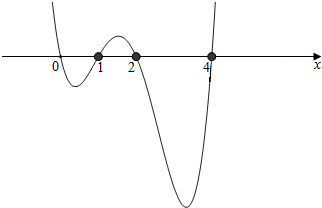 解:∵|x-1|<2,
解:∵|x-1|<2,
∴-2<x-1<2,
∴-1<x<3,
∴A=(-1,3),
∵$\frac{x(x-4)}{(x-1)(x-2)}$≤0,
∴x(x-1)(x-2)(x-4)≤0,且x=1,x=2,
利用穿根法,如图所示,
∴0≤x<1,2<x≤4,
∴B=[0,1)∪(2,4],
∴CUB=(-∞,0)∪[1,2]∪(4,+∞),
∴A∩B=[0,1)∪(2,3),
A∪B=(-1,4],
A∩(CUB)=(-1,0)∪[1,2].
点评 此题考查了交、并、补集的混合运算,熟练掌握交、并、补集的定义是解本题的关键.

练习册系列答案
相关题目
4.复数z=$\frac{1+i}{i}$(i是虚数单位)的共轭复数在复平面内对应的点是( )
| A. | (1,1) | B. | (1,-1) | C. | (-1,1) | D. | (-1,-1) |
1.ABCD-A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=$\frac{a}{3}$,过PMN的平面交上底面于PQ,Q在CD上,则PQ等于( )
| A. | $\frac{\sqrt{2}}{2}$a | B. | $\frac{\sqrt{2}}{4}$a | C. | $\frac{\sqrt{2}}{3}$a | D. | $\frac{2\sqrt{2}}{3}$a |
2.下列函数中既不是奇函数也不是偶函数的是( )
| A. | y=$\sqrt{{x}^{2}-2}$ | B. | y=ln(x+$\sqrt{{x}^{2}+1}$) | C. | y=x-ex | D. | y=$\frac{{e}^{2x}-1}{{e}^{x}}$ |