题目内容
3.已知sin(2α+$\frac{π}{3}$)=$\frac{2}{3}$,则sin(4α+$\frac{π}{6}$)的值是-$\frac{1}{9}$.分析 由sin(2α+$\frac{π}{3}$)=$\frac{2}{3}$,求出cos(4$α+\frac{2π}{3}$)=$\frac{1}{9}$,由此利用诱导公式能求出sin(4α+$\frac{π}{6}$)的值.
解答 解:∵sin(2α+$\frac{π}{3}$)=$\frac{2}{3}$,
∴cos(2α+$\frac{π}{3}$)=|$\sqrt{1-\frac{4}{9}}$|=|$\frac{\sqrt{5}}{9}$|,
∴cos(4$α+\frac{2π}{3}$)=cos2(2$α+\frac{π}{3}$)-sin2(2$α+\frac{π}{3}$)=$\frac{5}{9}-\frac{4}{9}$=$\frac{1}{9}$,
∴sin(4α+$\frac{π}{6}$)=cos[$\frac{π}{2}$-(4$α+\frac{π}{6}$)]=cos($\frac{π}{3}-4α$)=cos(4$α-\frac{π}{3}$)
=-cos(4$α+\frac{2π}{3}$)=-$\frac{1}{9}$.
故答案为:-$\frac{1}{9}$.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意二倍角公式和诱导公式的合理运用.

练习册系列答案
相关题目
10.不等式x+y>2所表示的平面区域是( )
| A. |  | B. | 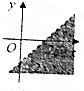 | C. |  | D. |  |
11.下列函数为偶函数的是( )
| A. | f(x)=x | B. | f(x)=x2 | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=x2-2x+1 |